استقرار
و عدم استقرار النواة
المــــــــــــــــادة
|
العلوم
الفيزيائية
|
المستوى
|
السنة
الثالثة ثانوي
|
الشعبة
|
علوم
تجريبية , رياضيات , تقني رياضي
|
نوع الملف
|
doc
|
صاحب الملف
|
|
تحميـــــــــــل
|
يمكنك تحميل الموضوع كاملا
من الرابط أعلاه أو قراءة نسخة معدلة منه مما يلي
|
- إستقرار و عدم إستقرار النواة :
- نموذج الذرة :
- تتكون الذرة من نواة تدور حولها الكترونات في مدارات محددة
- تتكون النواة من دقائق تسمى النويات (nucléons ) هما البروتونات الموجبة الشحنة و النيترونات المتعادلة كهربائيا
- تمثل نواة الذرة لعنصر كيميائي بالرمز AX حيث
X : رمز العنصر الكيميائي
Z : العدد الذري أو الشحني ( عدد البروتونات ) و هو مايميز كل عنصر عن غيره
A : العدد الكتلي وهو عدد البروتونات (Z) + عدد النيترونات (N) أي A = Z + N
N : يمثل عدد النترونات
- تتكون الذرة من نواة تدور حولها إلكترونات 99.99 % عبارة عن فراغ
- تكون كتلة الإلكترونات مهملة أمام كتلة النواة لهذا نقول أن كتلة النواة محتواة في نواتها
- النظائر :
هي ذرات لنفس العنصر لها نفس عدد البروتونات و تختلف في عدد النترونات
مثال : , 614C , 613C , 612C , 11H 13H , 12H
- إستقرار و عدم إستقرار النواة :
- تكون مكونات نواة الذرة متماسكة و متراصة فيما بينها رغم وجود القوى التنافرية الكهربائية البروتونات موجبة الشحنة و هذا بسبب وجود قوى أكبر من القوى التنافرية تدعى القوة النووية القوية
- إذا زاد عدد البروتونات تزداد القوى التنافرية و يمكن أن تتغلب على القوى النووية فتكون النواة في هذه الحالة غير مستقرة
- النشاط الإشعاعي :
2-1- لمحة تاريخية :
في سنة 1996 إكتشف العالم الفرنسي هنري بيكريل بالصدفة عند محاولة إكتشاف خصائص أشعة x المكتشفة حديثا من طرف العالم روتنغن أن أملاح اليورانيوم تصدرإشعاعات مختلفة عن أشعة x ثم إنكب العلماء من بعده على دراسة هذه الظاهرة الجديدة لتؤكد العالمة البولندية ماري كوري و زوجها بيير من عنصرا آخر يصدر نفس الأشعة هو عنصر البولونيوم سميت هذه الظاهرة بظاهرة النشاط الإشعاعي
2-2- دراسة الظاهرة :
النشاط الإشعاعي هو ظاهرة عشوائية ، لا يمكن التحكم فيها ولا إيقافها ، لا تتعلق بدرجة الحرارة ولا بالضغط ، تتحول خلاله نواة غير مستقرة (النواة الأب ) إلى نواة أخرى متولدة (النواة الإبن ) بإصدار إشعاعات
النواة المستقرة هي نواة تحافظ على مكوانتها ولا يحدث لها تفكك
أما النواة الغير مستقرة فهي نواة مشعة تصدر أشعة لتعطي في الأخير نواة أكثر استقرار مع اصدار أشعة α , β- ,β+ , γ نسمي هذه العملية بالتفكك الإشعاعي
مخطط سيقري : مخطط (N – Z )
بالرغم من القوة النووية القوية ، فضمن ال 1500 نواة المعروفة ( طبيعية أو إصطناعية ) ، يوجد فقط 260 نواة مستقرة ، البقية تتفكك تلقائيا لتتحول الى نواة أكثر إستقرار
نمثل إستقرار النواة بمنحنيين :  المسمى بمخطط سيقري أو
المسمى بمخطط سيقري أو 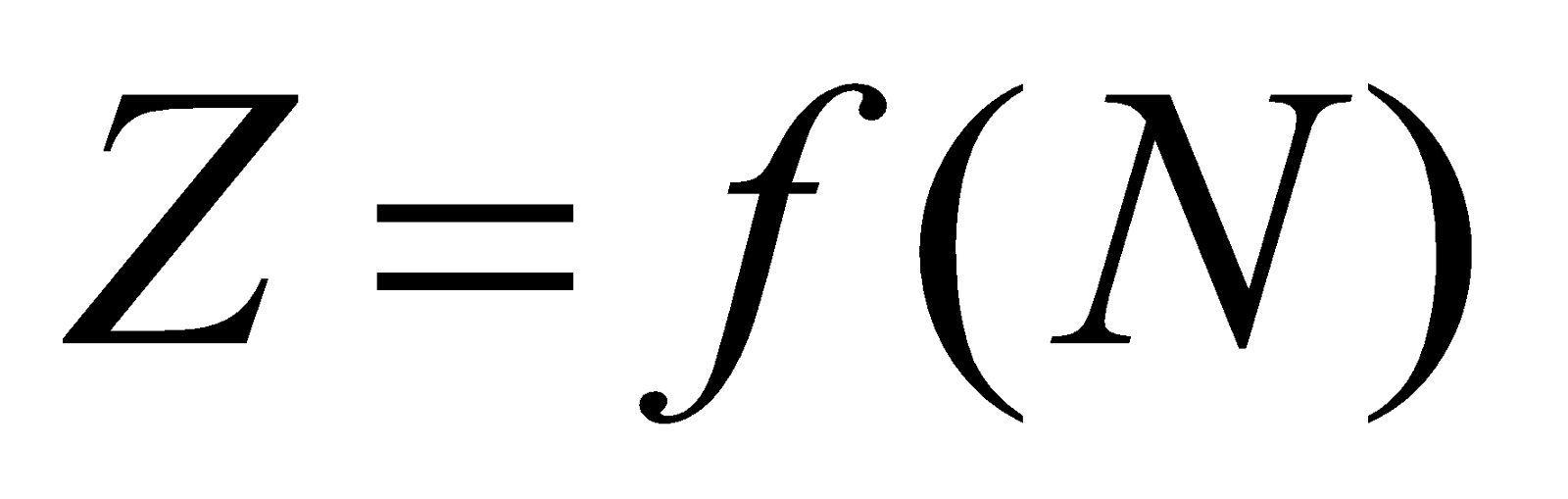 .
.
1- الأنوية المستقرة تشكل وادي الإستقرار ، ولا يوجد
نواة مستقرة من أجل Z>82 (الرصاص (Pb
- الأنوية الصادرة لجسيمات –β وهي الأنوية التي تقع فوق وادي الإستقرارلها فائض من النترونات . الممثلة باللون الأزرق
- الأنوية الصادرة لجسيمات +β وهي الأنوية التي تقع تحت وادي الإستقرارلها فائض من البروتونات . الممثلة باللون الأخضر
- الأنوية الصادرة لجسيمات α وهي الأنوية الثقيلة (Z>82) و التي تقع أقصى يمين واد الإستقرار الممثلة باللون الأصفر.
2-3- النشاط الإشعاعي α , β- ,β+ , γ
- قوانين الإنحفاظ :قانون SODDY
خلال تحول نووي يحدث إنحفاظ للكتلة و الشحنة أي للعدد الكتلي A والعدد الشحني Z حسب المعادلة
- - التفككات النووية :
- النشاط الإشعاعي α :
تصدر الأنوية الثقيلة  أشعة
أشعة  والتي هي عبارة عن أنوية الهيليوم
والتي هي عبارة عن أنوية الهيليوم  وتتحول إلى نواة لعنصر كيميائي آخر
وتتحول إلى نواة لعنصر كيميائي آخر
- ينقص العدد الكتلي ب 4 ، وينقص الرقم الذري ب 2 ( ينقص عدد النترونات ب 2)
- معادلة التفكك
- مثال :
- معادلة تفكك اليورانيوم :
- معادلة تفكك الرادون
خصائص إشعاعات آلفا α.
1-تحمل شحنتين موجبتين وكتلتها تساوي 4مرات كتلة الهيدروجين.
2-تسبب تأين الهواء الذي تمر به.
3-لها طاقة كبيرة.
4-قوة الاختراق ضعيفة , يمكن إيقافها باستخدام ورق عادية.
5-سرعتها أقل من سرعة الضوء
- النشاط الإشعاعي –β :
الأنوية لها فائض من النترونات يتحول نترون  إلى بروتون
إلى بروتون 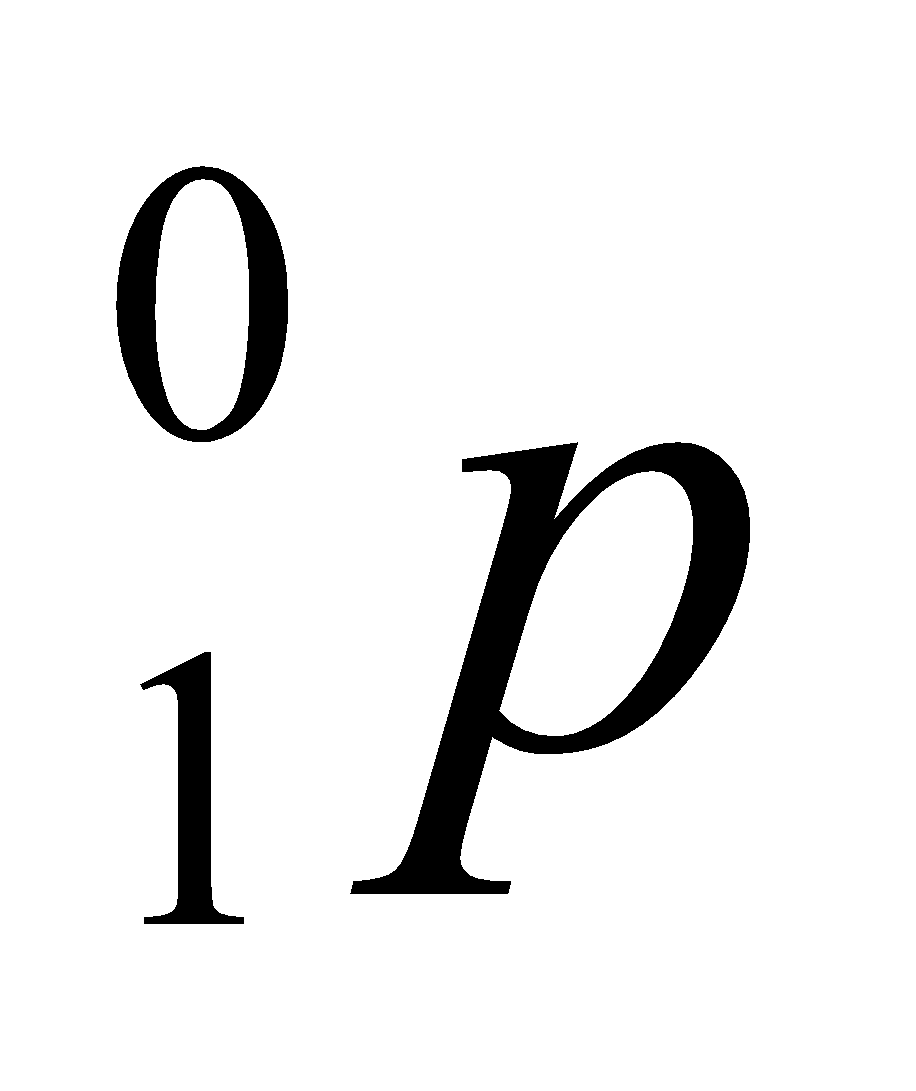 و تنبعث أشعة –β والتي هي عبارة عن إلكترونات
و تنبعث أشعة –β والتي هي عبارة عن إلكترونات  وفق المعادلة التالية :
وفق المعادلة التالية : 

- معادلة التفكك :
- مثال :
- معادلة تفكك الكوبالت
خصائص إشعاعات بيتاβ.
2- تسبب تأين الغاز الذي تمر به.
3- سرعتها تعادل سرعة الضوء
4- قوة الاختراق تعادل 100مرة من قدرة اختراق جسيمات آلفا.
5- يمكن إيقافها باستخدام الألواح من الرصاص.
ج- النشاط الإشعاعي +β :
الأنوية التي تحتوي على فائض من البروتونات يتحول بروتون 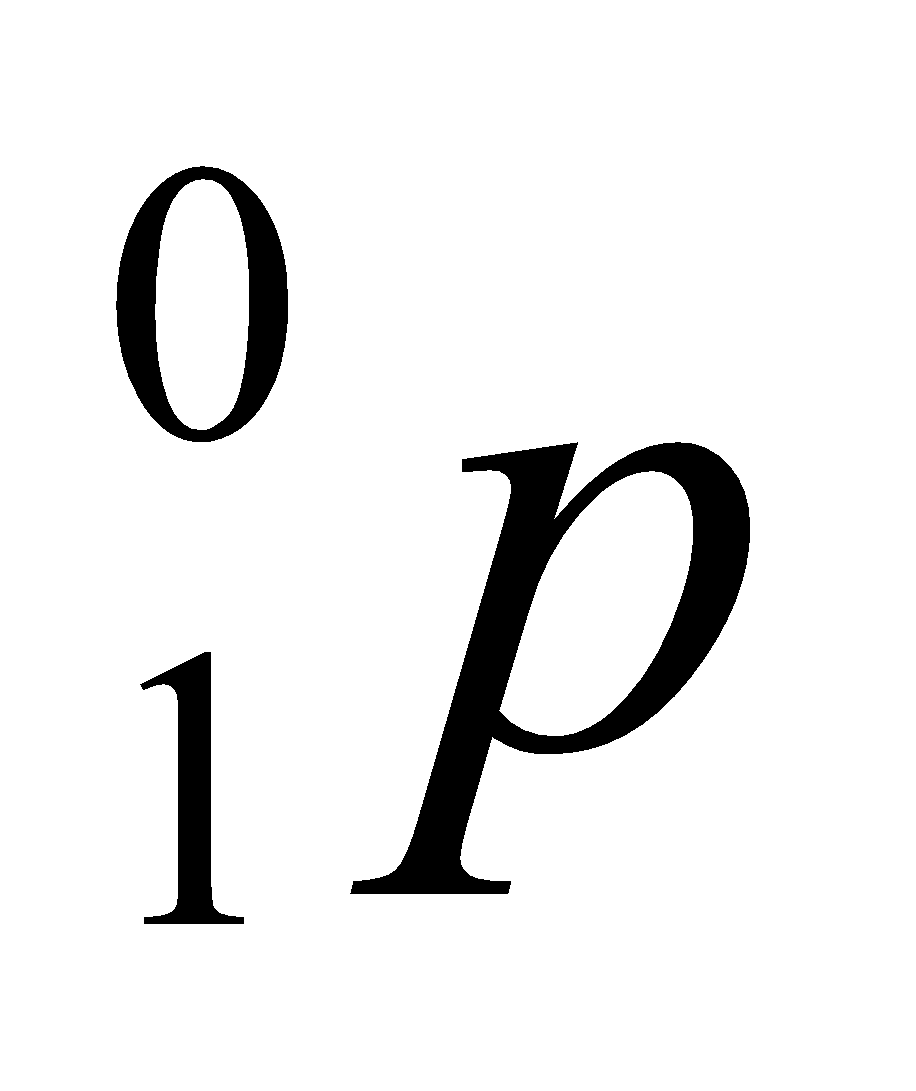 إلى نترون
إلى نترون  مع انبعاث جسيمات
مع انبعاث جسيمات 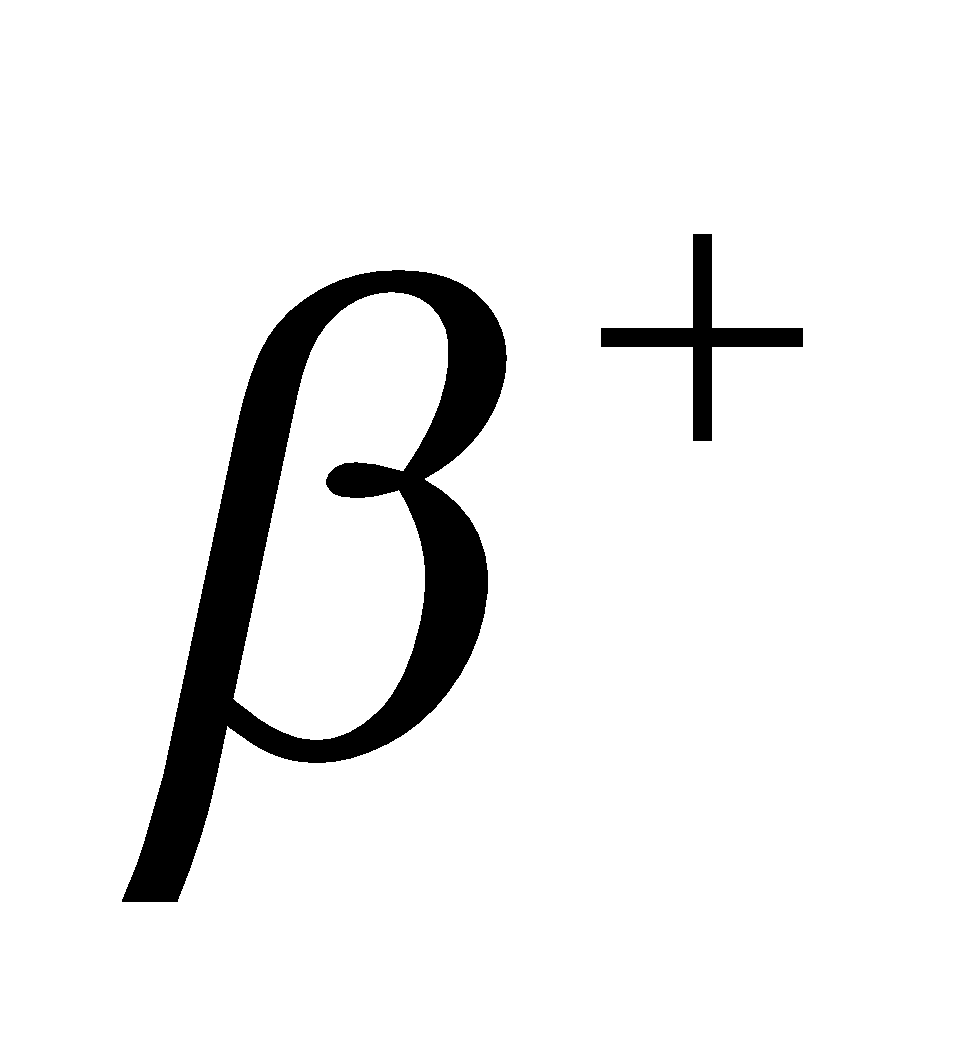 وهي عبارة عن الكترونات موجبة الشحنة
وهي عبارة عن الكترونات موجبة الشحنة  تدعى بوزيتونات وتتحول إلى نواة عنصر كيميائي آخر وفق المعادلة التالية
تدعى بوزيتونات وتتحول إلى نواة عنصر كيميائي آخر وفق المعادلة التالية 
- معادلة التفكك
معادلة تفكك الفوصفور 
الإصدار γ أو الإثارة المعاكسة :
عبارة عن موجات كهرومغناطيسية ذات طاقة كبيرة جدا، وهو نشاط يواكب الأنشطة الإشعاعية α و -β و +β ، حيث تكون النواة الإبن في حالة إثارة ZAX* ، تتخلص من فائض الطاقة بإصدارإشعاع γ.
معادلة هذا التحول النووي هي: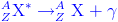 .
.
أمثلة
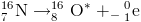 تفكك -β
تفكك -β
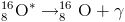
معادلة هذا التحول النووي هي:
أمثلة
الإشعاع γ يخترق  من الرصاص و عدة أمتار من الخرسانة .
من الرصاص و عدة أمتار من الخرسانة .
قدرة الإشعاع على التأيين ضعيفة مقارنة بقدرة الجسيمات α .
خصائص إشعاعات جاماδ.
1- لا تنحرف في وجود أي مجال كهربي أو مغناطيسي.( لأنة ليس لدينا شحنة)
2- قوة تأينها للغازات صغيرة.
3- سرعتها كبيرة تعادل سرعة الضوء.
4- قوة اختراقها كبيرة 10-100مرة قدرة أشعة بيتا.
5- تحتاج الى إيقافها باستخدام عدة سنتيمترات من الرصاص.
3- العائلة المشعة:
أثناء نشاط إشعاعي، تتحول نواة أصلية غير مستقرة إلى نواة متولدة ، تتحول بدورها إذا كانت غير مستقرة إلى نواة ثالثة. وهكذا دواليه إلى أن تتكون نواة مستقرة غير مشعة. مجموع النوى الناتجة عن نفس النواة الأصلية يسمى عائلة مشعة.
- التناقص الإشعاعي
- التناقص الإشعاعي
النشاط الإشعاعي ظاهرة طبيعية عشوائية
- قانون التناقص الإشعاعي
- لتكن N0 عدد الأنوية المشعة الإبتدائية ( t0=0 )
- لتكن N(t) عدد الأنوية المشعة المتبقية عند اللحظة t
يتناقص النشاط الإشعاعي لعينة مشعة بتناقص عدد الأنوية المشعة بمرور الزمن فيكون
ΔN = N(t) - N0 و هو مقدار سالب
أثبتت الدراسات الإحصائية أن المقدار ΔN لا يتعلق إلا :
- N(t) عدد الأنوية المتبقية
- Δt الزمن المعتبر
- وثابت يتعلق بنوع النواة λ ويسمى ثابت التفكك الاشعاعي وحدته مقلوب الزمن نكتب
ΔN = - λN Δt
إذا كان → 0 Δt تصبح العبارة
dN = - λN dt
dNdt + λN = 0
وهي معادلة تفاضلية من الدرجة الأولى حلها أسي من الشكل
N(t) = N0 e-λt
عدد الأنوية المشعة يتناقص وفق دالة أسية بمرور الزمن
- ثابت الزمن τ:
هو الزمن اللازم لتفكك 63%من الأنوية المشعة الموجودة في العينة حيث : 
زمن نصف العمر t1/2:
زمن نصف العمرt1/2 ، هو المدة الزمنية اللازمة لتفكك نصف العينة الإبتدائية
|
ومنه
المماس للبيان عند 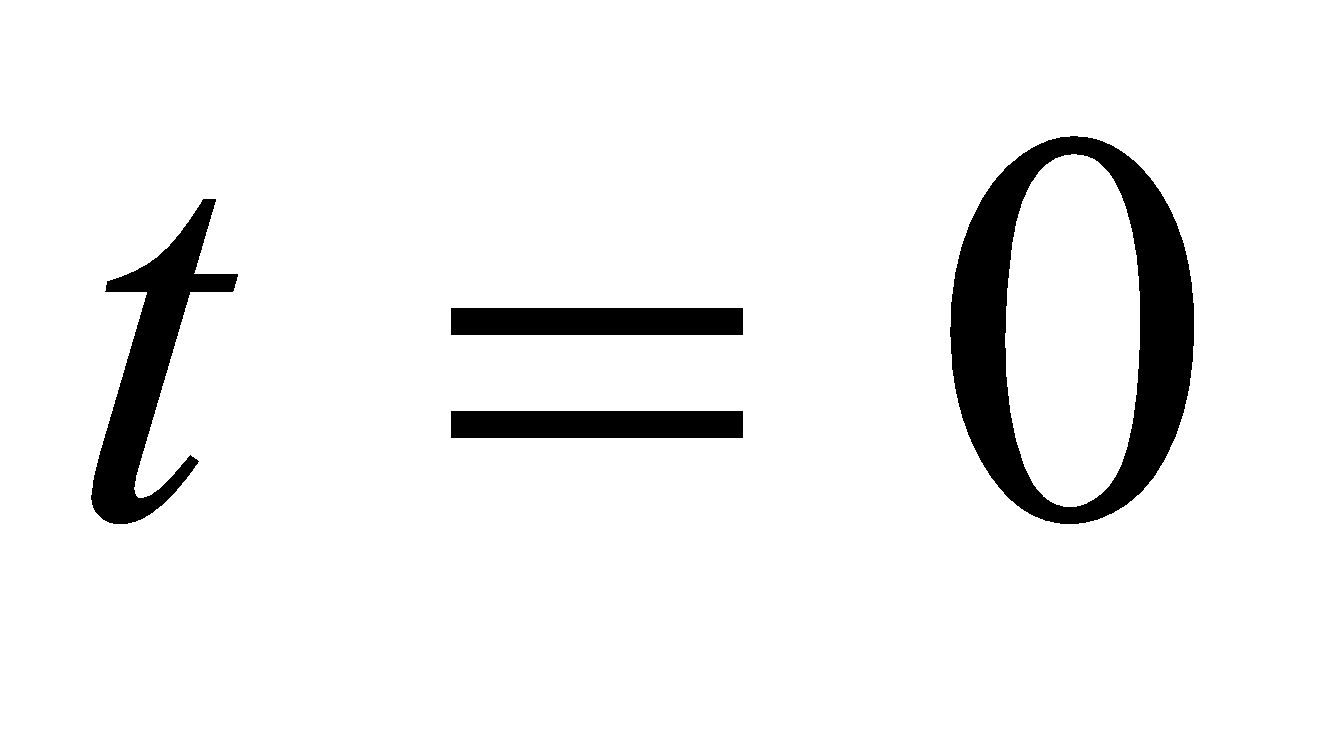 يقطع محور
يقطع محور
الأزمنة عند اللحظة  .
.
ملاحظات :
1-
n t1/2
|
……..
|
3 t1/2
|
2 t1/2
|
t1/2
|
0
|
t
|
N0/2n
|
……..
|
N0/23
|
N0/22
|
N0/2
|
N0
|
N(t)
|
2- مدة التناقص تساوي 
- نشاط عينة مشعة :
يعرف نشاط منبع مشع، بسرعة تفكك المنبع أي عدد الأنوية المتفككة في وحدة الزمن. وحدته تسمى البيكريل (Bq) حيث : A = - ΔNΔt
إذا كان Δt صغير جدا
النشاط 7 :
1- عبر عن النشاط اللحظي لعينة  بدلالة عدد الأنوية اللحظي
بدلالة عدد الأنوية اللحظي  و ثابت النشاط الإشعاعي
و ثابت النشاط الإشعاعي  .
.
2- إستنتج عبارة  بدلالة
بدلالة  ،
،  و
و  حيث
حيث  هو نشاط العينة عند اللحظة
هو نشاط العينة عند اللحظة  .
.
3- - إستنتج عبارة  بدلالة
بدلالة  ثابت التفكك حيث
ثابت التفكك حيث  ،
،  و
و  .
.
الأجوبة :
1-
2-
عند اللحظة  يكون
يكون  وبالتعويض في المعادلة العامة نجد :
وبالتعويض في المعادلة العامة نجد :
3-