العالم الاسلامي السنة الأولى ثانوي

درس الدرات الكهربائية التيار المتناوب  السنة الثانية ه ك

المــــــــــــــــادة	الهندسة الكهربائية
المستوى	السنة الثانية ثانوي
الشعبة	تقني رياضي
نوع الملف	doc
صاحب الملف
تحميـــــــــــــل	درس التيار المتناوب وثيقة الأستاذ درس التيار المتناوب وثيقة التلميذ

يمكنك تحميل الموضوع كاملا من الرابط أعلاه أو قراءة نسخة معدلة منه مما يلي " وثيقة الأستاذ "

الدارات الكهربائية في التيار المتناوب

عناصر الدرس :

التيارات الدورية

 المقادير المشتركة: الدور، التردد، القيم اللحظية،  العظمى، المنتجة، المتوسطة

التيار المتناوب الجيبي

العلاقات الرياضية: الدور، التردد، القيمة اللحظية والمنتجة

تمثيل فرينل

قانون أوم في التيار المتناوب الجيبي

 الدارة  م– ذ- سالتسلسلية، توازي وكيفي

التجاوب

الاستطاعة في التيار المتناوب الجيبي

نظرية بوشرو

مفاهيم أولية في التيار المتناوب الثلاثي الطور

العلاقات الرياضية

المقادير البسيطة والمركبة

تمهيد  رأينا سابقا أنه أمكننا  إنتاج قوة محركة كهربائية عندما غيرنا كمية التدفق العابر لوشيعة :

تجربة

دوران الوشيعة  بسرعة زاوية w  مع  مغناطيس ثابت ينتج تغيير في مساحة S أي تغيير في التدفق  Φوبالتالي تغيير في الحقل B ، تظهرإذا قوة محركة كهربائية متحرضة e  يمكن قياسها بجهاز فولط متر.

دوران المغناطيس بسرعة زاوية w  مع  وشيعة ثابتة ينتج عنه تغيير في التدفق Φ وبالتالي تغيير في الحقل B ، تظهرإذا قوة محركة كهربا ئية متحرضة e  يمكن قياسها بجهاز فولط متر.

بعد إكتشاف التيار المستمر ، نلاحظ أنه يوجد نوع ثاني من التيار وهو تيار متغير كون التدفق متغير .

2- أنواع الإشارات الكهربائية : تنقسم الإشارات إلى قسمين :

- إشارة ( تيارأوتوتر) مستمرة : وهي الإشارة التي لاتتغيرعلى مدى الزمن و تحدد بمعرفة قيمتها (شكل 1).

- إشارة ( تيار أو توتر ) متغيرة :  وهي الإشارة التي تتغير مع الزمن وتتمثل في أنواع بحيث تكون معرفة حسب طبيعة تغيراتها مع الزمن ( شكل 2) .

تصنيف التيارات : تصنف التيارات حسب إتجاه دورانها :

أ)- تيارات أحادية الإتجاه : تنتقل دائما في نفس الإتجاه أي بنفس الإشارة ، تكون سالبة أو موجبة ( شكل3).

ب)- تيارات ثنائية الإتجاه : لاتنتقل دائما في نفس الإتجاه أي لديها شدة تارة موجبة و تارة سالبة ( شكل4).

ج)- تيارات دورية : تيار متغير يسمى دوري لما يأخذ نفس القيمة خلال الفترتين t1  و t1+nT ( هناك تكرار لشكل مطابق خلال زمن ثابت  T ) حيث :

t1 : لحظة معينة

n  : عدد طبيعي

T  : هو عبارة عن مجال زمني يسمى بالدور (Période)، وحدته الثانية ( s ) .

مثال : في الجزائر توزيع التيار دوري في الشبكة دوره  T=20ms .

التردد : (Fréquence) التردد لتيار دوري هو عبارة عن عدد دورات خلال ثانية .

                     وحدة التردد هي الهرتز Hertz ( Hz)

                    

مثال : شبكة توزيع تيار كهربائي في الجزائر توزع تيار تردده f=50Hz  .

المقادير الكهربائية المميزة للإشارات : قيم التوتر u(t) و تيار i(t)  الناتج عن تيار متغير تتغير قيمها في كل لحظة .لتمييز تيار نعرف :

• قيم عظمى ترمز بـ  Î ,Û
• قيم متوسطة ترمز بـ Ū، Ī  أو ,
• قيم فعالة أو منتجة ترمز بـ I ,U

أ)- القيمة العظمى : وهي القيمة العظمى التي تأخذها الدالة (u(t  أو (i(t  والتي تسمى كذلك بقيمة الذروة يمكن قياسها بجهاز راسم الإهتزاز .

ب) – القيمة المتوسطة : يمكن تعريفها بمقارنة مع تيار المستمر حيث أن شدة التيار المتوسطة لتيار متغير تساوي إلى شدة التيار المستمر الذي يحمل نفس كمية شحنة الكهربائية Q خلال نفس المدة الزمنية .

يمثل الشكل المقابل تيار مستمر شدته I .كمية الكهرباء Q

التي ينقلها تمثل في المساحة A لمستطيل  obcd خلال زمن t

إذن المساحة A  = كمية شحنة الكهربائية Q

القيمة المتوسطة Ī تساوي :

ليكن » شكل 5 «  حيث مساحة A2 هي مساحة المستطيل obcd

و A1 مساحة المضلع obefcd .

التيار المتغيرi(t)  ينقل كمية كهرباء ممثلة في مساحة A1

المساحةA2  تمثل كمية كهرباء التي تنقل من طرف التيار المستمرI

إذا كانت مساحة A1= مساحة A2  إذن I  هي القيمة المتوسطة

لتيار المتغير i(t) .

ملاحظات:

القيمة المتوسطة لتيار دوري معرفة خلال دور .

بالنسبة لتيار ثنائي الإتجاه المساحات الموجودة تحت المحور الأفقي تحسب سالبا .

تيار ذو قيمة متوسطة معدومة يعتبر متناوب Alternatif أي مساحة النوبة الموجبة تساوي مساحة النوبة السالبة .

تقاس القيمة المتوسطة لتيار متغير بجهاز آمبير متر كهرومغناطيسي في وضعية مستمر وتكون القراءة مباشرة

ج) القيمة الفعالة أو المنتجة : الشدة الفعالة لتيار متغير تساوي شدة التيار المستمر الذي ينتج في نفس المقاومة R وخلال نفس المدة الزمنية t إنتشار الحرارة W= R i2 t  و التي تمثل أيضا القيمة المتوسطة لـ i2(t) .
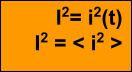
أي

لحساب القيمة الفعالة I لتيار i بواسطة منحنى i(t) نرسم أولا i2(t)  ثم نحسب القيمة المتوسطة لـ i2(t) أي < i2 >  .

مثال : حساب القيمة المتوسطة لـتيار المستطيل i(t)  شكل 6 .

القيمة المتوسطة لـ i(t)  هي :   

  إذن (i(t  تيار متناوب .

القيمة الفعالة لـ (i(t هي :

  

د)- تيار جيبي متناوب : نقول أن تيار متغير جيبي إذا كانت عبارته الرياضية من شكل :

حيث : i(t) قيمة اللحظية لشدة التيار أو السعة اللحظية وحدتها الآمبير .

Î : قيمة العظمى للشدة التيار وتسمى السعة أو المطال الأعظمي وحدتها الآمبير.

ω : النبض أو السرعة الزاوية للمطال وحدتها راديان على الثانية rad/s .

(ω t + φ) : الطور أو الصفحة اللحظية وهي عبارة عن زاوية متغيرة مع الزمن وحدتها الراديان  (rad).

φ  : الطور الإبتدائي أي الزاوية في اللحظة  t = 0s وحدتها الراديان .

  -1 ≤  sin (ω t +  φ ) ≤  1    .

نسمي القيمة ذروة ذروة القيمة   2 Î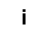

النبض ، الدور و التردد :

نضع θ=ω t  . الدالة i(t) = Î  sin (θ +  φ )

دورها يساوي 2π  إذن لدينا :

ω :  rad / s

T: بثواني s

f  : تردد بـ Hz

* القيمة المتوسطة :  القيمة المتوسطة لتيار متناوب

جيبي معدومة .

القيمة الفعالة : القيمة الفعالة لتيار متناوب جيبي

تساوي حاصل قسمة القيمة العظمى على :  أي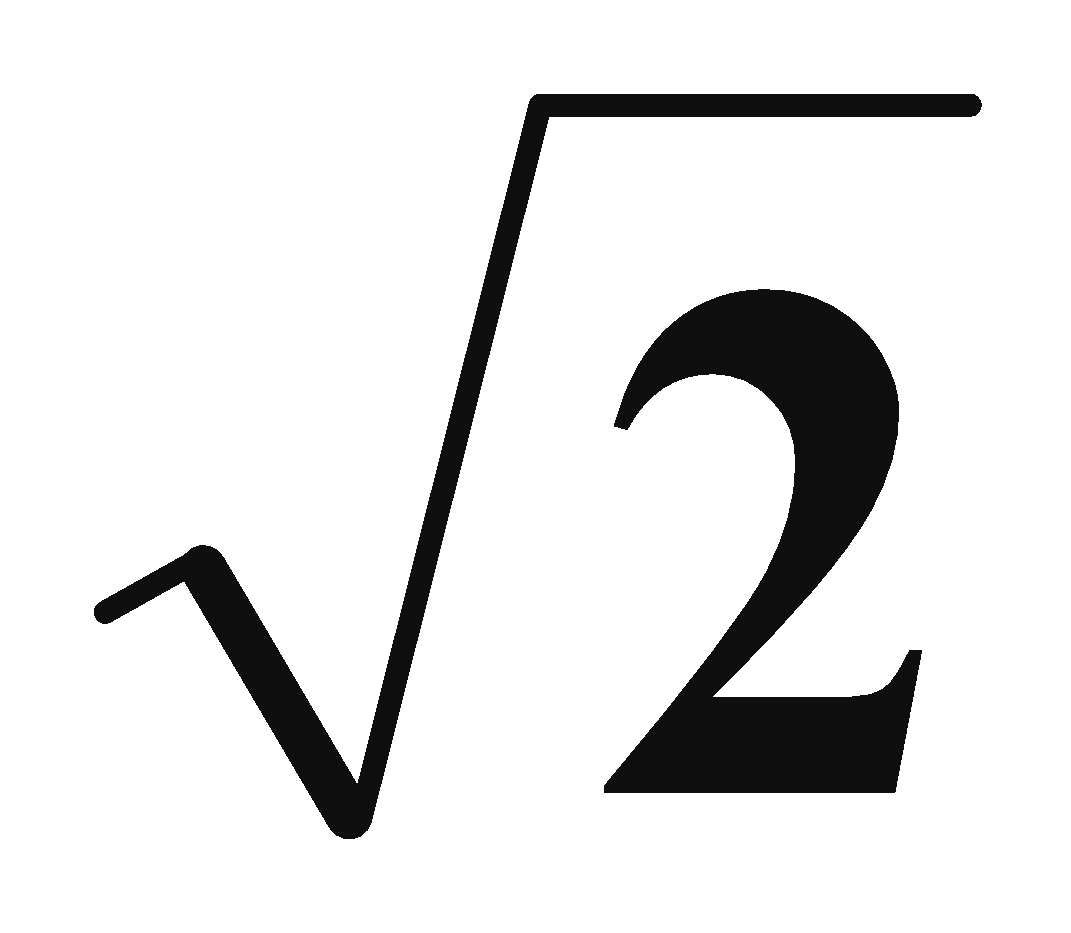

                   

 عمليا القيم u  و i معرفة بالقيم الفعالة لذلك نقول شبكة  v 220  معناه القيمة الفعالة تساوي 311
 

3- تمثيل فرنل :
هو عبارة عن تمثيل شعاعي لدوال جيبية بحيث يسمح بإستبدال دالة جبيبة بشعاع هدفه:

- مقارنة دالتين جيبيتين بنفس تردد.

- جمع دوال جيبية بنفس التردد .

* شعاع فرنل :

لكل مقدار جيبي u(t)= Ûsin(ωt+φ)   نضم شعاع  OM  حيث :

- طاولة شعاع OM  تساوي إلى قيمة العظمى للمقدار الممثل :  =Û||OM|| .

- الزاوية (ox,oM0)  تمثل الصفحة أو الطور الإبتدائي أي لماt=0s  وضعية Mعند M0 أي φ=(ox,oM0)

- الزاوية (ox,oM) تمثل الصفحة أو الطور اللحظي أي في لحظة t  وضعية النقطة M  .

(ox,oM)= (ox,oM0) + ( oM0,oM)= ωt+φ               

ليكن m مسقط M على محور oy .

om= u(t)= Ûsin(ωt+φ)  

لذلك نقول أن التوتر الجيبي u(t)= Ûsin(ωt+φ)  يمثل بشعاع دوار oM  حيث oM=U    =Û   

سرعة دورانه = ω .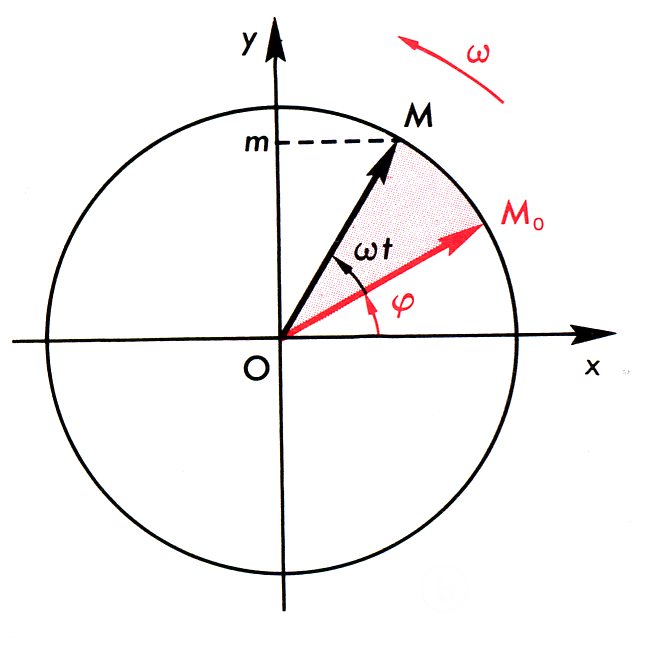

* دوران شعاع و التمثيل الديكارتي:

(u(t)= Ûsin(ωt+φ
Û||= OM||
 

* ممانعة ثنائي القطب غير فعال وخطي:

ثنائي قطب غير فعال وخطي هوعبارة عن دارة لاتحتوي على قوة محركة كهربائية ، و وسائطها لها قيم ثابتة مثل مكثفة C – وشيعة L – مقاومة R  .

إذا غذينا ثنائي القطب بتوتر جيبي u(t)= Ûsin(ωt+φ)  يجتازه تيار i(t) = Î  sin (ω t)   فإن القيم الفعالة U  وI  تتناسب طرديا . نضع :

                   

حيث Z يمثل الممانعة الحقيقية لثائي القطب ، وحدتها آوم Ω كمقاومة .

العلاقة السابقة هي نفسها قانون آوم في المستمر  U=R I لكن يوجد فرقين بينهما هو :
U  و I يمثلان القيمة الفعالة في المتناوب و في التيار المستمر المقادير هي نفسها .

R ثابتة لكن Z تبقى ثابتة إذا لم يتغير التردد f .    

مقلوب الممانعة تسمى بالمسامحة

وحدتها Ω-1  أو سيمنس  .

قانون آوم لمختلف الدارات الكهربائية :

مقاومة R صرفة :

(i(t) = Î  sin (ω t

(u(t)= Ûsin(ωt+φ  

التيار i  و التوتر u  على توافق في صفحة  

 Z= R  و φ=0   .   

تمثيل فرنل: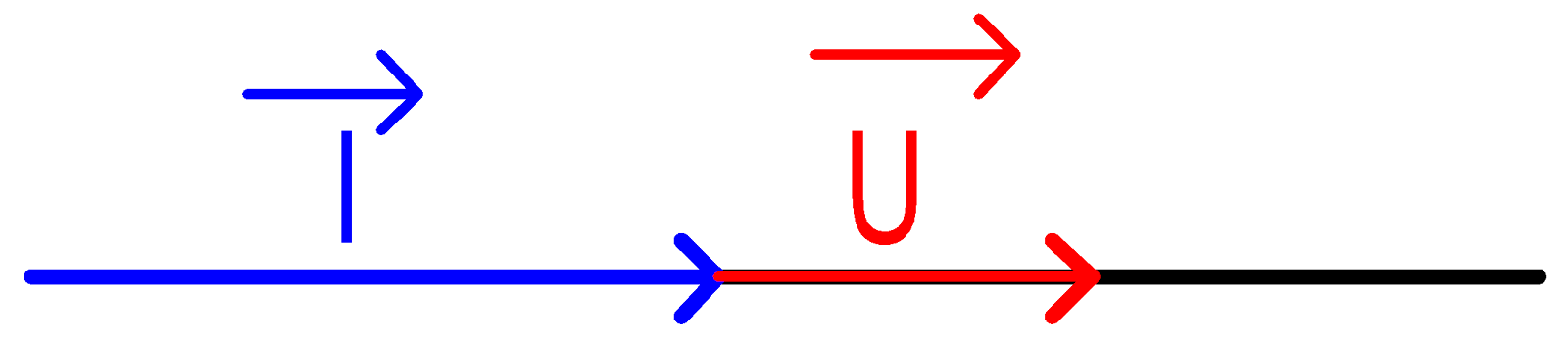               

* وشيعة مثالية  L:  

التوتر u  على ترابع متقدم بالنسبة لتيار i

Z= L ω    و  

تمثيل فرنل :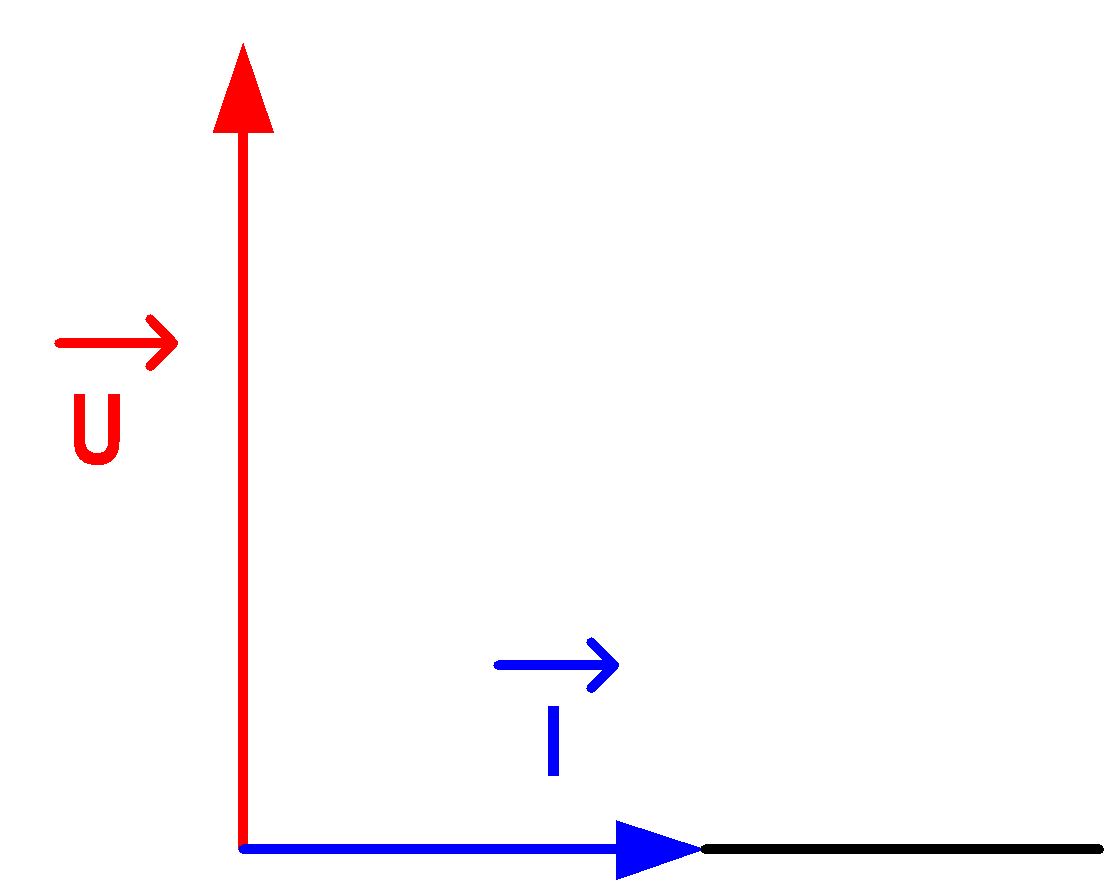

* مكثفة C :  

التوتر u على ترابع متأخر بالنسبة لتيار i  

                 و  

تمثيل فرنل :

* مقاومة R  و وشيعة L على التسلسل :

تمثيل فرنل :

* مقاومة R و وشيعة L و مكثفة C على التسلسل:

حالة 1 :



          
  فعل الوشيعة يغلب فعل المكثفة ( دارة حثية )

حالة 2:



فعل المكثفة يغلب فعل الوشيعة ( دارة سعوية ).

φ<0 span="">

حالة 3:   



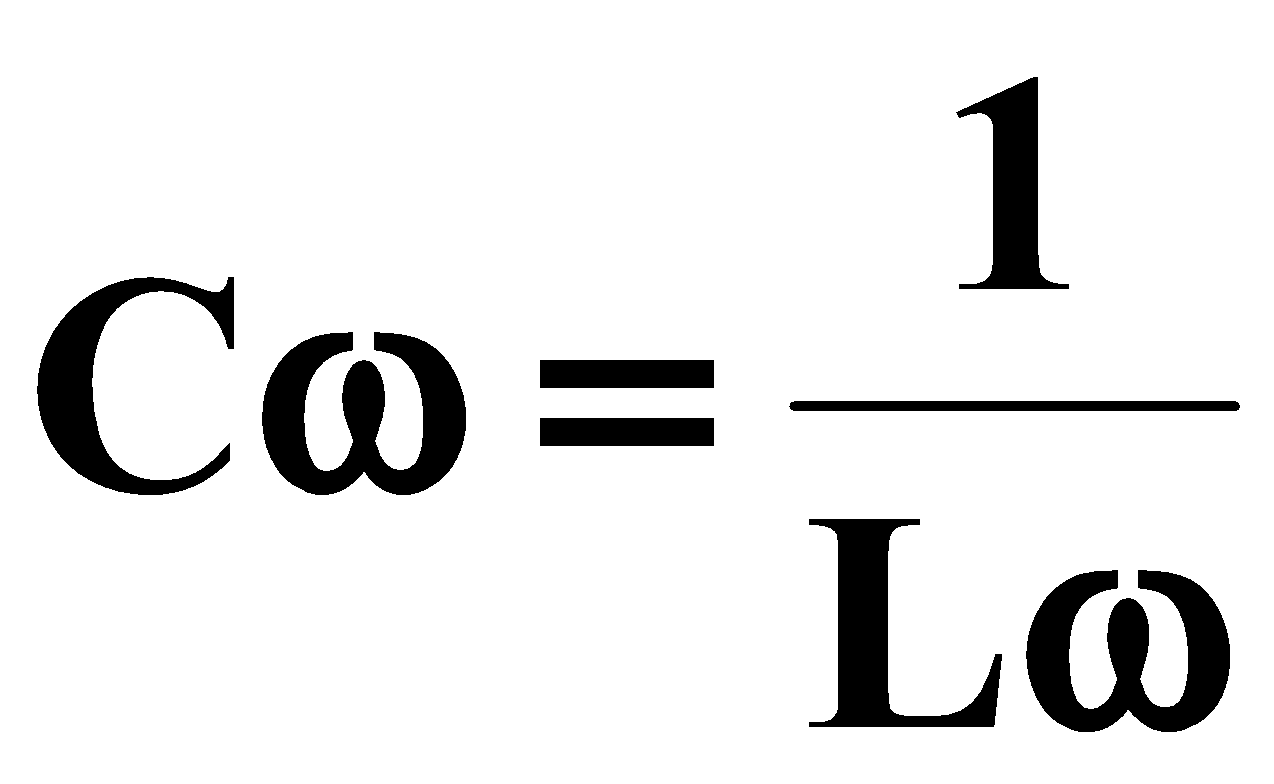
فعل مكثفة يساوي فعل وشيعة  ( حالة تجاوب) .

ممانعة التركيب و فرق الصفحة :

                                       

* خصائص التجاوب :
عند تجاوب لدينا :

يمكننا الحصول عليه إما :
- تثبيت التردد f و ذاتية L وتغيير السعة C  .
- تثبيت التردد f و السعة C و تغيير الذاتية L .
- تثبيت السعة C و الذاتية L  و تغيير التردد f  أو النبض ω .

* نتائج التجاوب : لما  عند 0ω نبض التجاوب  لدينا   Z= R  هذا يستلزم :

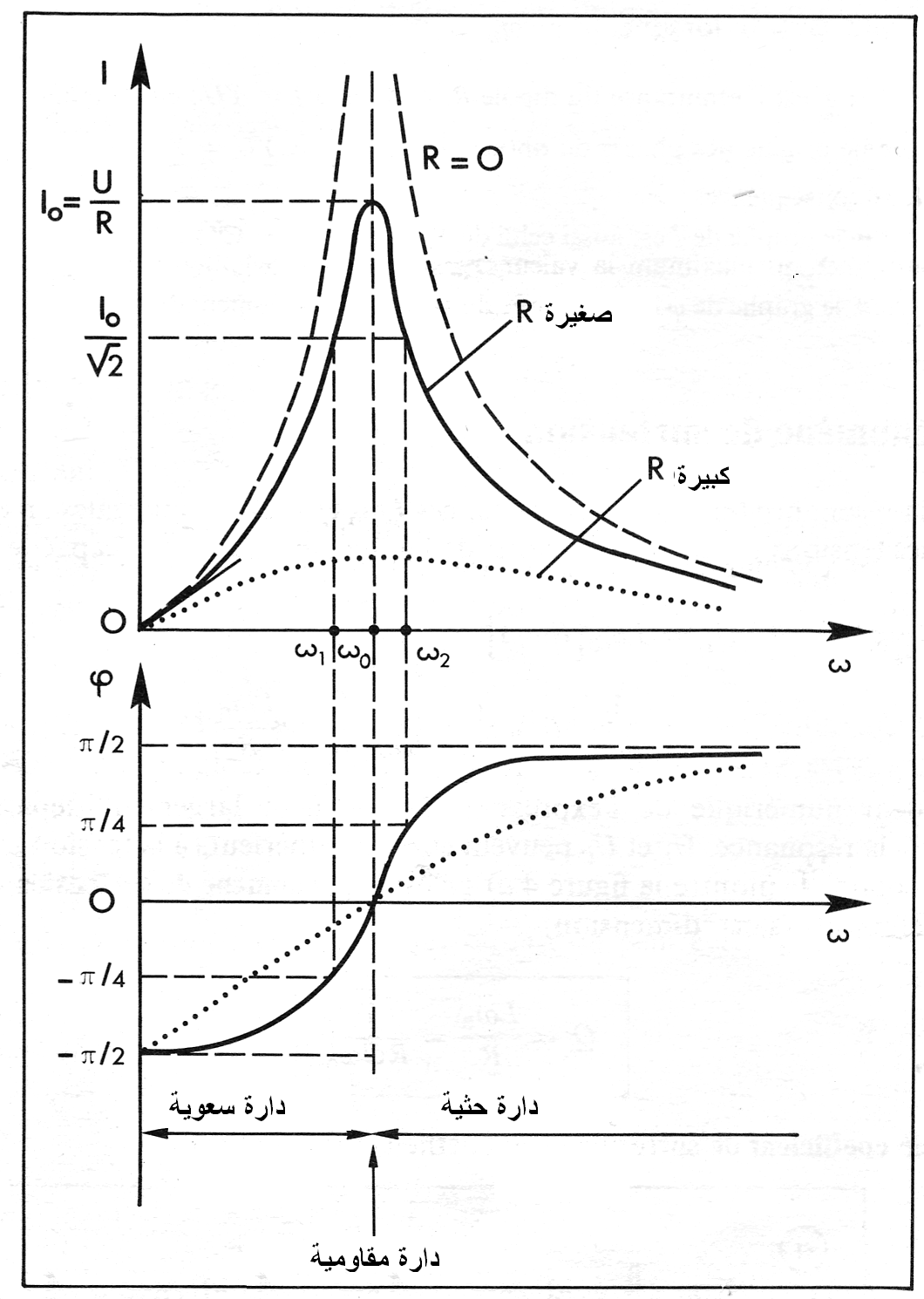
- الدارة RLC تكافؤ دارة تحتوي على مقاومة  R .

- شدة التيار تكون أعظمية .

φ=0 -  فرق الصفحة يكون معدوم أي  uو i

على توافق في الصفحة .

- uC و uL على تعاكس في الصفحة

أي فرق الصفحة بينهما يساوي π

* منحنى التجاوب :

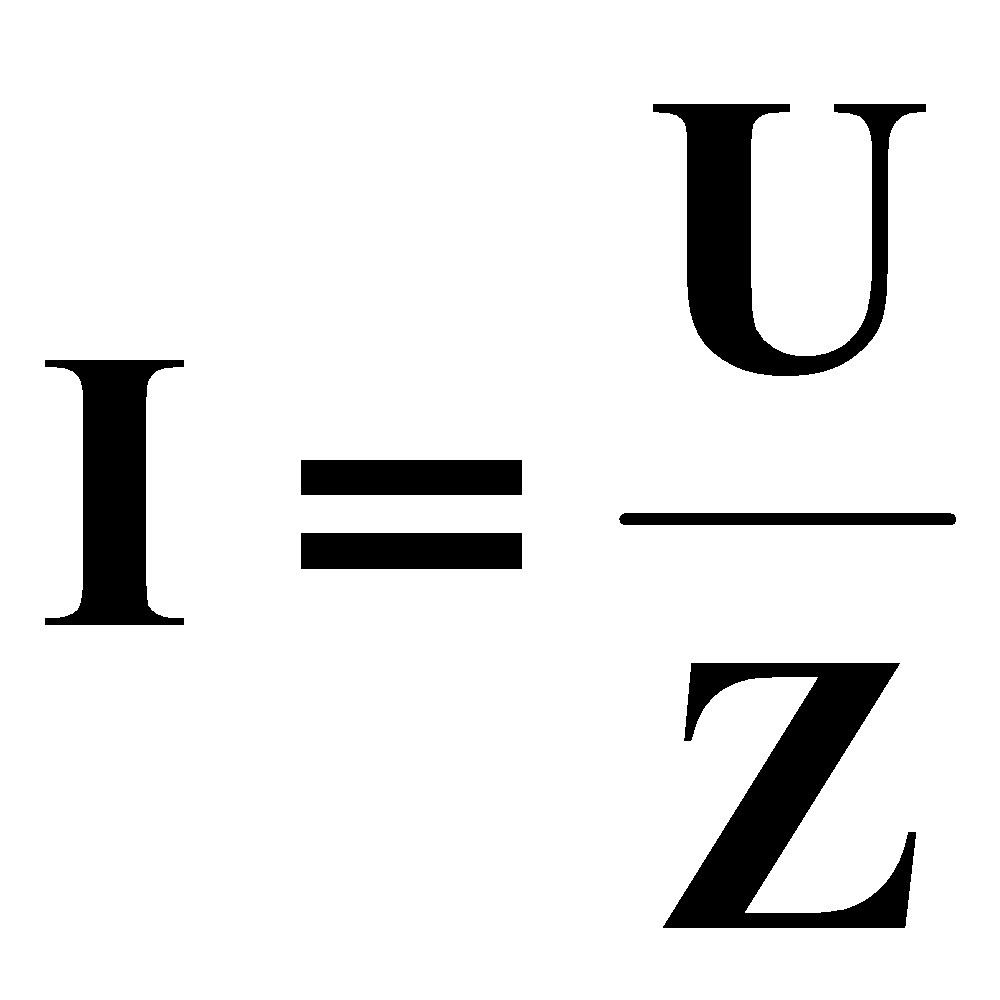
I= f(ω) ,                   ,φ= f(ω         

عصبة العبور( شريط الإمرار):

* دارة  RLC على التوازي :

i = iL + iR + iC

دارة سعوية i متقدم عن u (φ>0)	دارة حثية i متأخرعن u (φ<0 span="">	حالة تجاوب i وu على توافقφ=0

عبارة المسامحة :   

عبارة فرق الصفحة :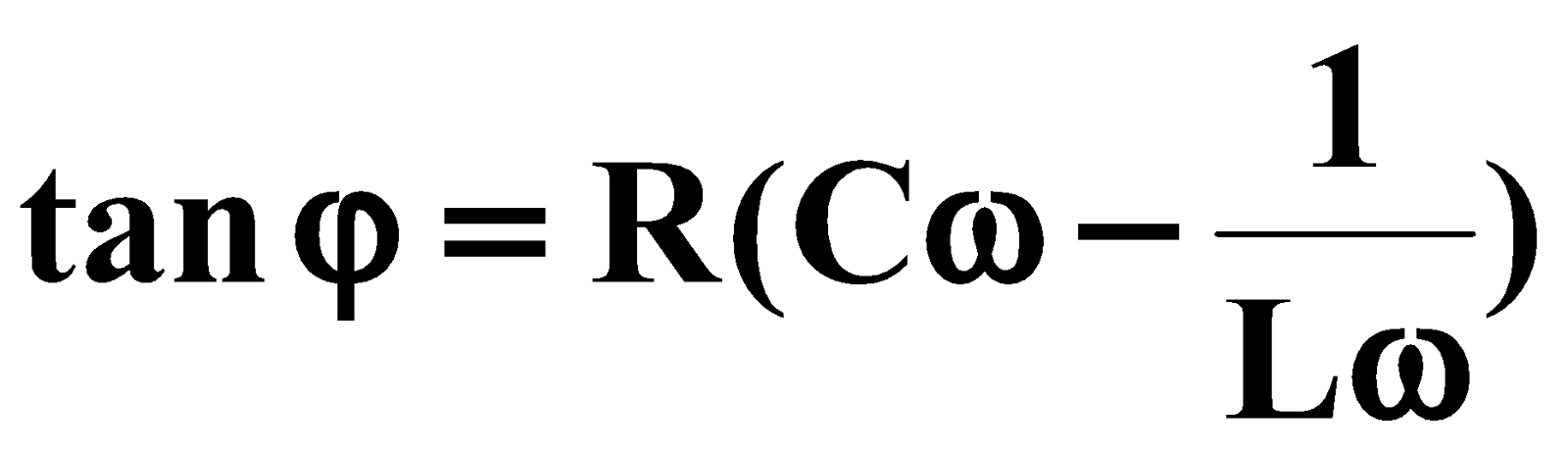

4- الإستطاعة في التيار المتناوب الجيبي:

4-1 الإستطاعة اللحظية :
نعرف الإستطاعة اللحظية بالجداء :p= u i     وحدتها الواط (W)

مع : u(t)=U     sin(ωt+φ) و   sin(ωt)    i(t)= I

4-2 الإستطاعة الفعالة :
هي القيمة المتوسطة للإستطاعة اللحظية وحدتها كذلك الواط (W)

-  إذا كان ثنائي القطب مستقبل ( مثلا محرك) لدينا : P>0  ⇐ cosφ>0   ⇐    -π/2<φ<+π/2.

- إذا كان ثنائي القطب عبارة عن مولد ( منوب) لدينا : P<0 cos="" nbsp="" span="">

ملاحظة : cosφ  يمثل عامل الإستطاعة .

مثال : دارة تحتوي على مقاومة R : لدينا φ=0 ⇐ cosφ = 1 ⇐ P= U I  مع U= R I  ⇐ P=R I2

المقاومة تستهلك على طول الطاقة الكهربائية .

4-3 الإستطاعة الظاهرية : تعرف بالجداء

  وحدتها فولط آمبير (VA)  وهي تميز بعض

الآلات التي تعمل في النمط الجيبي مثل المحولات و المنوبات  .

4-4 الإستطاعة الردية أو الإرتكاسية:  :  تعرف بـ            وحدتها فولط آمبير ردي var

5 العلاقة مابين الإستطاعات :

  

 

مثال : ثنائي القطب عبارة عن دارة RLC على التسلسل :

العناصر	الإستطاعة الفعالة P(watts)	الإستطاعة الرديةQ(vars)	ملاحظات
R	RI2	0	R تستهلك الإستطاعة الفعالة
L	0	LωI2	L  تستهلك الإستطاعة الردية
C	0		C تنتج الإستطاعة الردية

6- نظرية بوشرو :

أ- نص النظرية : في دارة كهربائية تحتوي على مستقبلات( أجهزة) تجتازها تيارات جيبية .

- الإستطاعة الفعالة الكلية المستهلكة تساوي إلى مجموع الجبري للإستطاعات  الفعالة المستهلكة من طرف كل جهاز .

- الإستطاعة الردية الكلية المستهلكة تساوي إلى مجموع الجبري للإستطاعات  الردية المستهلكة من طرف كل جهاز . نقول إذن أن هناك حفاظ للإستطاعات الفعالة و الردية .

ب- طريقة بوشرو : هذه الطريقة الحسابية تسمح بوضع حصيلة إستطاعات فعالة وردية والتي يمكن تمثيلها  في جدول :

الآخذات	الإستطاعة الفعالة P(watts)	الإستطاعة الردية Q(vars)
ثنائي القطب 1	P1	Q1=P1 tanφ1
ثنائي القطب2	P2	Q2= P2 tanφ2
الشبكة	P=P1+P2	Q=Q1+Q2

يمكن إذن حساب التيارأوالتوتر الكلي للشبكة بإستعمال العلاقات التالية: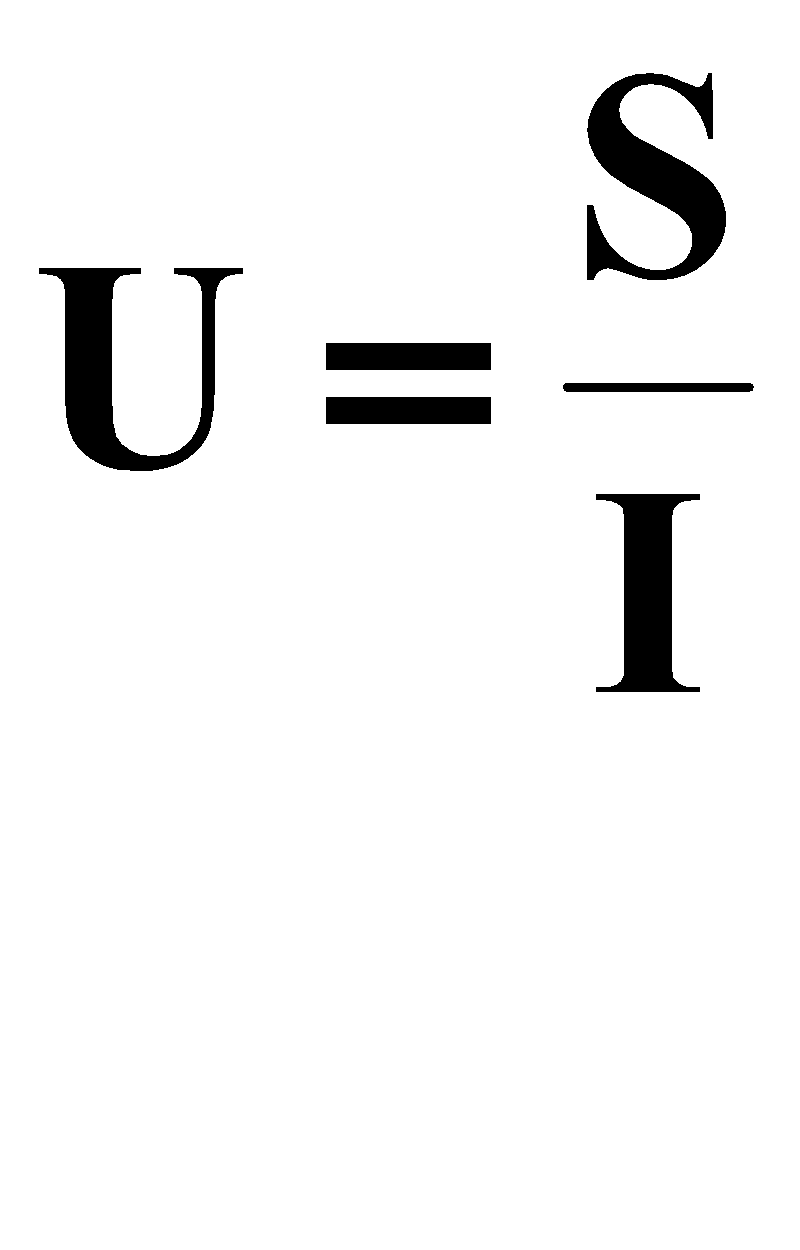

                                                                

7- التيار المتناوب ثلاثي الطور:

7-1 توترات البسيطة و توترات المركبة:

أ) – تعريف :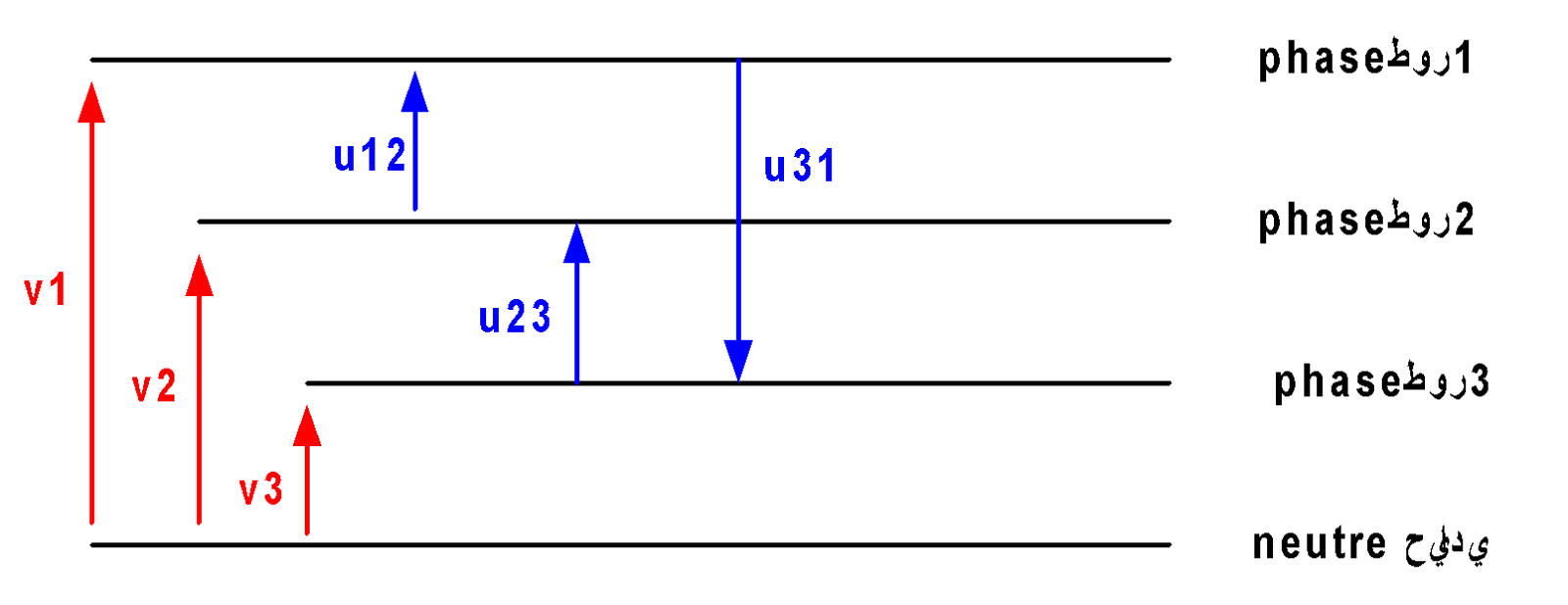

التوترات البسيطة : v1,v2,v3 هي التوترات الموجودة مابين طور و حيادي . في النمط المتوازن لدينا :

V1=V2=V3=V= 220v  لمأخذ شبكة .

التوترات المركبة : u12 ,u23 ,u31 هي التوترات الموجودة مابين طور و طور . في نمط المتوازن لدينا:

U12=U23=U31 = U= 380v  لمأخذ شبكة .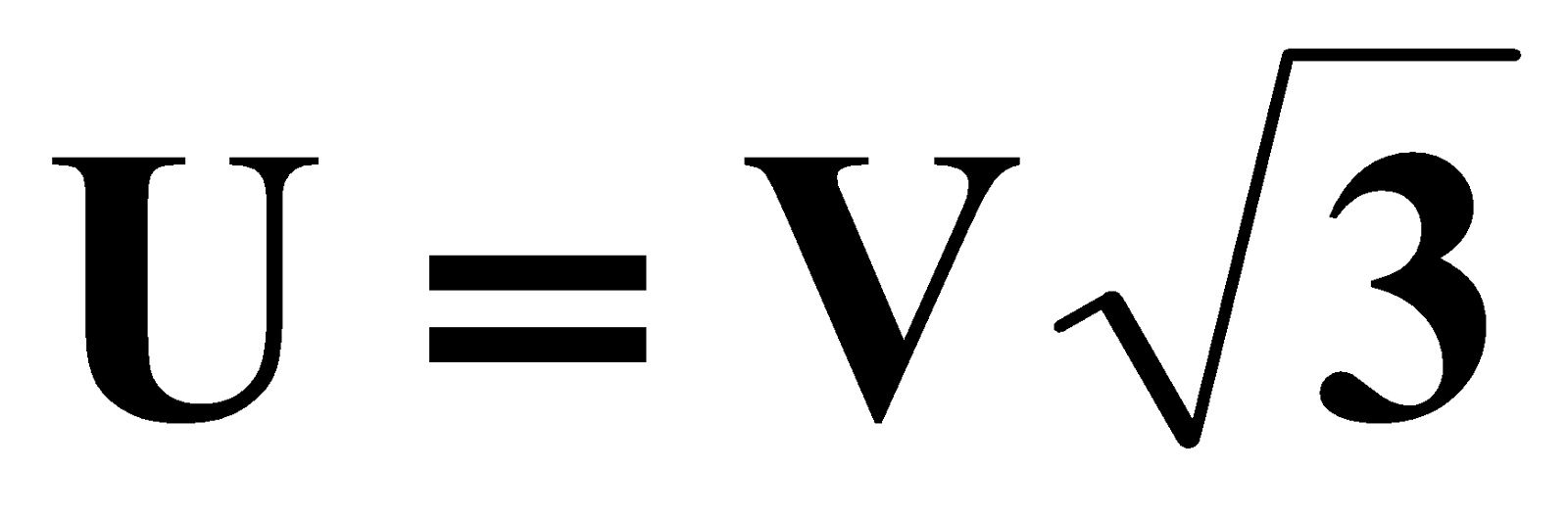    

لدينا :       u31 = v3-v1 u12= v1-v2    ;    u23= v2-v3    ;

ب)- تمثيل بياني:

ج)- تمثيل فرنل :