درس الدارة
المغناطيسية: تطبيق على المرحل الحقل المغناطيسي
المـــادة
|
الهندسة الكهربائية
|
المستوى
|
السنة الثانية ثانوي
|
الشعبة
|
تقني رياضي
|
نوع الملف
|
doc
|
صاحب الملف
|
|
تحميــــل
|
يمكنك تحميل الموضوع كاملا
من الرابط أعلاه أو قراءة نسخة معدلة منه مما يلي
"
وثيقة الأستاذ "
|
عناصر الدرس :
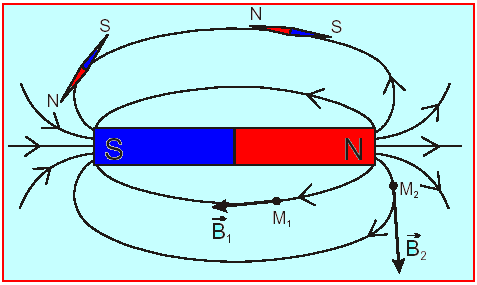
- الحقل المنتج
بمغناطيس دائم: خطوط المجال والطيف
- الحقل المنتج
بالتيار المستمر في سلك، وشيعة مسطحة، و حلازونية
التحريض المغناطيسي
في: -
سلك
- وشيعة مسطحة
- وشيعة حلازونية
التدفق المغناطيسي
قانون لابلاس: تطبيقه
على المحرك
قانون فارادي: تطبيقه
لإنتاج الكهرباء
قانون لنز
التحريض الذاتي الحديدي
المغناطيسي

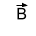
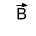



2- الحقل المغناطيسي الناتج عن تيار كهربائي :
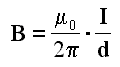










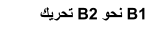










ع
الدارات المغناطيسية و آلة التيار المستمر
1- الحقل المغناطيسي :
11- – تعريف : يمكن تحديد مكان الحقل المغناطيسي في نقطة P من الفضاء بشعاع B(P) له الخصائص التالية :

- الحامل : هو حامل إبرة ممغنطة موضوعة في نقطة P .
- الاتجاه : هو الاتجاه من الجنوب (S) إلى الشمال (N) لهذه الإبرة .
- الشدة : هي طويلة شعاع الحقل المغناطيسي وحدتها تسلا tesla (T) .
1-2 – قياس الحقل المغناطيسي :
تقاس شدة الحقل المغناطيسي بواسطة جهاز التيسلامترTeslamètre
الوحدة العالمية لشدة الحقل المغناطيسي B هي التسلا و يرمز لها بالحرف (T) .
مثال : أمام مغناطيس دائم نحصل على حقول بعشرات الميلي تسلا .
1 -3 – خطوط الحقل و الطيف المغناطيسي :
نسمي خط الحقل المغناطيسي المنحنى المماسي عند كل نقطة للشعاع B و في نفس الاتجاه .
الطيف المغناطيسي هو مجموعة خطوط الحقل لحقل مغناطيسي .
عند كل نقطة من الحقل المغناطيسي ، يوجد شعاع B واحد فقط بحيث :
- لايتقاطع خطا حقل أبدا .
- يوجد في الحقل ، عدد لامتناهي من خطوط الحقل
2-1 تجربة آرستد ŒRSTED (1820):
ناقل من النحاس AB مربوط بمولد و مشدود فوق إبرة ممغنطة SN موازية للناقل. تكون عندما القاطعة k مفتوحة ( حالة شكل a ) .
- عند غلق القاطعة k : التيار يمر من A نحو B فتنحرف الإبرة ( حالة شكل b ) .
- عند قلب أقطاب المولد يمر التيار من B نحو A فتنحرف الإبرة في الاتجاه المعاكس ( حالة شكل c ).
النتيجة : التيار الكهربائي هو عبارة عن منبع للحقل المغناطيسي .
2- الحقل المغناطيسي الناتج عن تيار كهربائي :
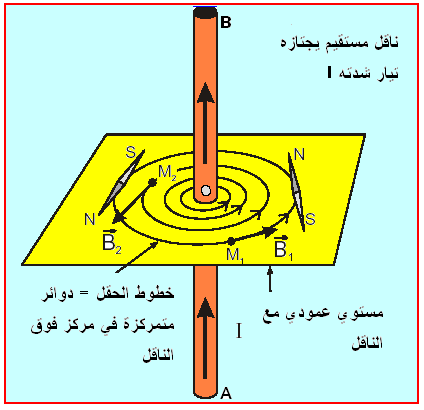
-22 ناقل مستقيم :
- تكون خطوط الحقل بجوار الناقل
عبارة عن دوائر مركزها النقطة o.
- تكون الإبرة الممغنطة مماسيةلخطوط الحقل .يتعلق اتجاه الحقل المغناطيسي
باتجاه التيار الكهربائي.
2-2-1 تعيين اتجاه خطوط الحقل : تدل الإبرة الممغنطة على جهة خطوط الحقل ، و هناك عدة قواعد عملية لمعرفة هذه الجهة .
أ- قاعدة مراقب آمبير : المراقب المستلقي على طول الناقل بحيث يدخل التيار من قدميه و يخـرج من رأسه ، يرى خطوط الحقل موجهة نحو يساره .
ب- قاعدة ساحبة الفلين لماكسويل :
tire-bouchon de Maxwell
جهة الخطوط هي الجهة التي يجب أن ندير إليها ساحبة الفلين بحيث يتقدم في جهة التيار .
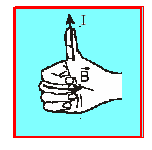
ج- قاعدة اليد اليمنى : اليد اليمنى تحيط بالناقل بحيث يشير الإبهام إلى جهة التيار ، فتعطينا
جهة الأصابع الأخرى جهة خطوط الحقل
2-2-2- شدة الحقل المغناطيسي : 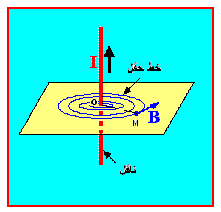
شدة الحقل المغناطيسي في نقطة M تبعد بمسافة
OM=d عن ناقل مستقيم يجتازه تيار شدته I هي:
حيث :
μ0 :هو ثابت و يمثل النفاذية المطلقة في الخلاء في النظام الدولي للوحدات μ0=4π10-7 SI
I : شدة التيار المار في الناقل وحدته آمبير A
d : المسافة مابين الناقل و نقطة M وحدتها المتر .
B : شدة الحقل وحدته التسلا T.
2-3 ناقل دائري ( وشيعة مسطحة ) :
ناقل على شكل لفة دائرية يسمى بحلقة والحقلالمغناطيسي الناتج حوله يكون ممركزا داخل الحلقة و تكون خطوط الحقل مستقيمة .
2-3-1 اتجاه خطوط الحقل:
* يمكن تعيين اتجاه خطوط الحقل باستعمال لإبرة الممغنطة .
* يمكننا استعمال القواعد السابقة (رجل آمبيرواليد اليمنى ).
* جهة خطوط الحقل هي جهة تقدُّم ساحبة الفلين عندما نديرها في جهة التيار .
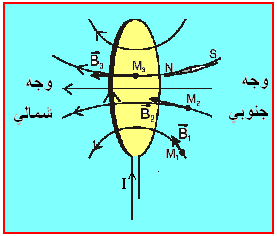
* يمكننا استعمال طريقـة خاصة بالوشائع لمعرفة وجهي الوشيعة الشمالي NORD و الجنوبي SUD وهذا حسب اتجاه التيار (انظر الشكل الآتي) .
2-3-2 شدة الحقل المغناطيسي : شدة الحقل المغناطيسي في مركز وشيعة مسطحة تحتوي على N لفة دائرية قطرها D ويعبرها تيار شدته I هي : 
2-4 وشيعة طويلة (حلزونية) : solénoïde
هي وشيعة يكون طولها L كبيرا أمام نصف قطرها R
خطوط الحقل في الداخل موازية لمحور الحلزونية ( الحقل المغناطيسي منتظم ) .
2-4-1 اتجاه خطوط الحقل : نحصل عليه بتطبيق نفس قواعد وشيعة مسطحة .
2-4-2 شدة الحقل المغناطيسي : شدة الحقل المغناطيسي بجوار مركز حلزونية مكونة من N لفة متلاصقة و مرتبة على طول L و يجتازها تيار شدته I هي :
مع n= N/L و يمثل كثافة الحلقات أي عدد الحلقات في المتر .
ملاحظات :
- تكون العلاقة صحيحة في كل نقطة داخل الوشيعة إذا كان طولها غير متناهي .
- داخل وشيعة حقيقية تكون القيمة صحيحة بالقرب من المركز و ذلك إذا كان طول الوشيعة L أكبر نسبيا من قطر اللفات .
3- التدفق المغناطيسي : نضع داخل حقل
مغناطيسي منتظم شعاعه B ، سطحا مساحته S.
لتوضيح وضعية السطح بالنسبة للحقل المغناطيسي :
- نختار شعاع الوحدة n الناظم على السطح S
- نعتبر الزاوية : ( n,B )= α .
عبارة التدفق المغناطيسي عبر سطح هي :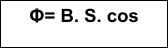
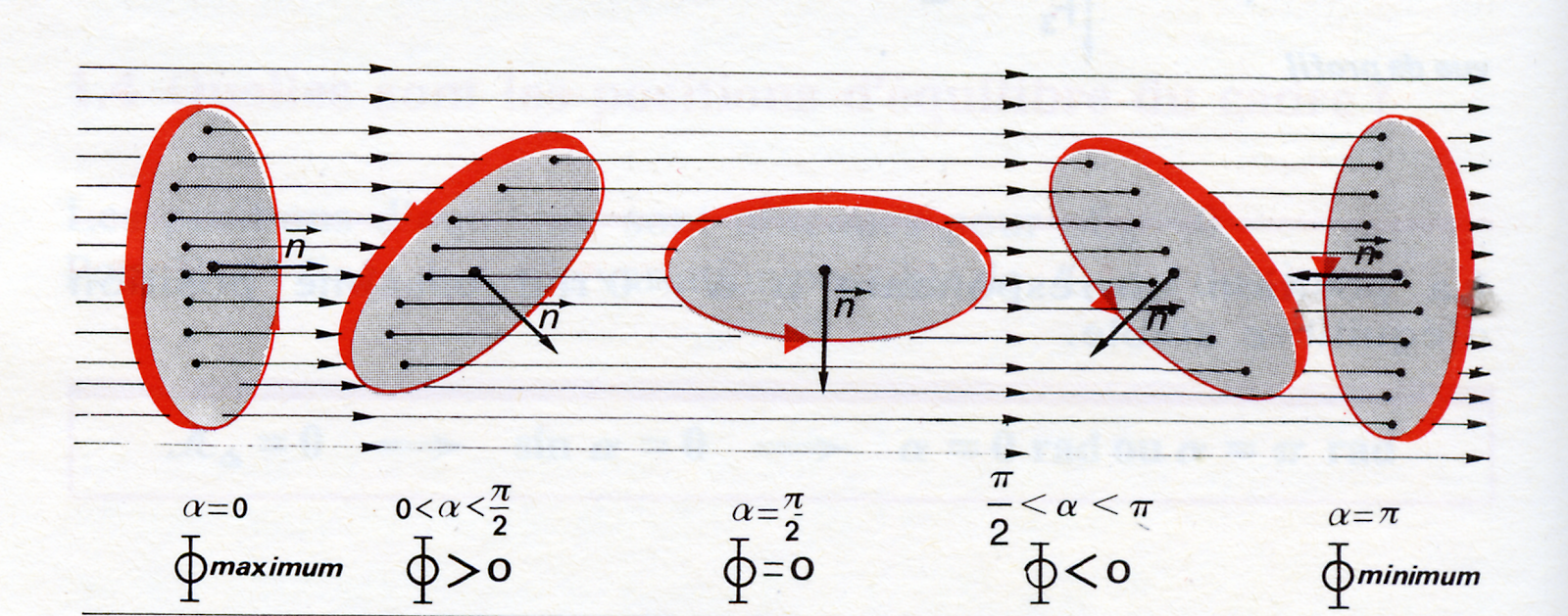
3-1 خصائص التدفق المغناطيسي :
* التدفق المغناطيسي هو مقدار جبري .
* العبارة Φ= B.S cosα تبين أن إشارة Φ تتعلق بإشارة cosα
- يشير التدفق المغناطيسي إلى عدد خطوط الحقل التي تعبر الدارة .
- ترتبط إشارة التدفق بالاتجاه الذي تعبُره خطوط الحقل.
- يكون التدفق موجبا إذا عبرت خطوط الحقل الدارة في نفس اتجاه الناظم n .
3-2 وحدة التدفق المغناطيسي في النظام الدولي (SI) .
وحدة التدفق هي " الويبر " Weber (Wb) و هو التدفق الذي يعبر سطحا مستويا مساحته واحد متر مربع عندما يكون عموديا على خطوط حقل منتظم قيمته واحد تسلا .
4قانون لابلاس :Laplace 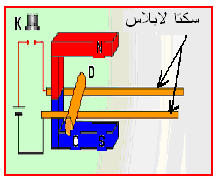
4-1 تأثير حقل مغناطيسي على ناقل يعبره تيار كهربائي :
أ- تجربة سكتي لابلاس :
عند الضغط على الزر K ، وبوجود حقل مغناطيسي
منتظم B ومرور التيار شدته I على الناقل الموضوع
فوق السكتين ينتقل الناقلCD من جهة .
- عند عكس أقطاب المولد ينعكس اتجاه الناقل .
- عند عكس أقطاب المغناطيس ينعكس أيضا اتجاه التاقل .
استنتاج :
كل ناقل يجـتازه تيار كهربائي وهو موجـود داخل حقل مغناطيسي ، فإنه يخضـع لقوة F تسـمى القـوة الكهرومغناطيسية ( قوة لابلاس ) .
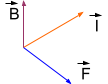
5-2 مميزات القوة الكهرومغناطيسية :
* نقطة التأثير : هي من منتصف الناقل CD
* الحامل : عمودي على الناقل وعلى شعاع الحقل المغناطيسي، أي أنه عمودي على المستوي المتكون منهما.
* الجهة : تتعلق بجهة التيار و جهة الحقل المغناطيسي وتُعيَّن بقاعدة رجل آمبير أو قاعدة اليد اليمنى.
قاعدة رجل آمبير : تكون جهة القوة F وفق يسار رجل آمبير المستلقي على الناقل بحيث يدخل التيار من رجليه و يخرج من رأسه وهو ينظر في جهة شعاع الحقل المغناطيسي B .

قاعدة اليد اليمنى : تكون جهة القوة وفق الإبهام العمودي على كل من السبابة التي تشير إلى جهة التيار الكهربائي I والوسطى التي تشير إلى جهة الحقل المغناطيسي B. 
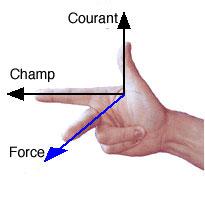
* الشدة : تتناسب مع :
- شدة الحقل المغناطيسي B .
- شدة التيار المار في الناقل I .
- طول الناقل L .
- sin α حيث α : الزاوية المحصورة بين الشعاع B و الناقل .
وحدة القوة الكهرومغناطيسية نيوتن .
ملاحظة : يمكن تمثيل شعاع عمودي على مستوي الشكل بالطرقة التالية :
6- تطبيقات قانون لابلاس :
6-1 محرك كهربائي صغير :(تجربة عجلة بارلو)
عند غلق القاطعة k يجتاز التيار نصف قطر
العجلة ، وهي موضوعة داخل حقل مغناطيسي
منتظم ، فتصبح خاضعة لقوة كهرومغناطيسية F
تكون نقطة تأثير هذه القوة هي منتصف الجزء
المغمور في الحقل المغناطيسي .
قوة لابلاس الناتجة تمد عزم بالنسبة لمحور العجلة وبالتالي تدور .
تمثل هذه الظاهرة المبدأ الأساسي لمحركات التيار المستمر
إذا محرك تيار مستمر يحتوي على عنصرين أساسيين :
- الساكن stator ويمثل المحرض أي مولد للحقل المغناطيسي ( عبارة عن وشيعة مغذية بتيار مستمر).
- الدوار rotor ويمثل المتحرض أي العنصر الخاضع للحقل والذي يحمل نواقل لدورانه نتيجة خضوعها لقوى كهرومغناطيسية .
7- التحريض الكهرومغناطيسي :
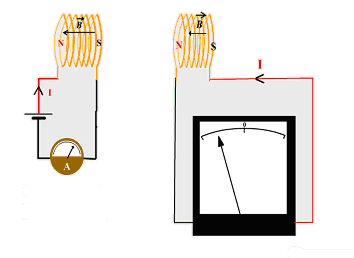
التجربة 1:
التفسير:
- إنحراف إبرة المقياس الغلفاني تدل على أنه خاضع لفرق كمون ،ويجتازه تيار مصدره الوشيعةB2 .
- أصبحت الوشيعةB1 مقرا لقوة محركة كهربائية متحرضة .
- عندما نقرب الوشيعةB1 من الوشيعةB2 ، تجتازها كمية متزايدة من خطوط الحقل و تصبح منقولة نحو جهة يكون فيها الحقل أكبر ، تزداد القيمة المطلقة للتدفق المحتضن من طرف الوشيعة خلال هذا الإنتقال ، و بالعكس عندما نبعد الوشيعةB1 عن الوشيعة B2 ، تنقص القيمة المطلقة للتدفق المحتضن .
- تدعى هذه الظاهرة بـ : ظاهرة التحريض الكهرومغناطيسي و يسمى التيار الناشـىء بالتيـار المتحرض ، كما تسمى الوشيعةB1 بالمحرض و الوشيعة B2 بالمتحرض .
8- قانون فرادي :
يولد كل تغير في التدفق من خلال دارة كهربائية قوة محركة كهربائية متحرضة e.
تجربة 2 : مبدأ تشغيل محول مع Bيتغير على مدى الزمن .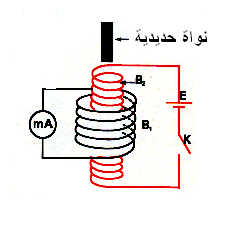
الو شيعة المحرضة B2 يجتازها تيار دائم شدته I ،
المتحرض الو شيعة B1 موصولة بجهاز آمبير متر
أنظر شكل . ندخل نواة حديدية داخل وشيعة B2 ،
نلاحظ ظهور تيار متحرض على جهاز آمتير متر .
إن النواة الحديدية توجه خطوط الحقل داخل الوشيعة
وبتالي تقوي نفاذية μ ، الحقل و التدفق يزداد .
تغيير في التدفق ينتج قوة محركة كهربائية f.é.m متحرضة e و تيار متحرض .
تجربة 3 :- نقرب القطب الجنوبي للمغناطيس الدائم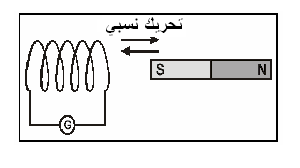
نحو الوشيعة ثم نبعده .
- نقرب القطب الشمالي للمغناطيس الدائم نحو الوشيعة
ثم نبعده
التفسير : حركة المغناطيس تولد في دارة الوشيعة تيار
متحرض هذا الأخير ينتج في الوشيعة تدفق مغناطيسي
يسمى تدفق متحرض ، يكون إتجاهه بحيث يعاكس
تحركات المغناطيس أي تغيرات التدفق المحرض .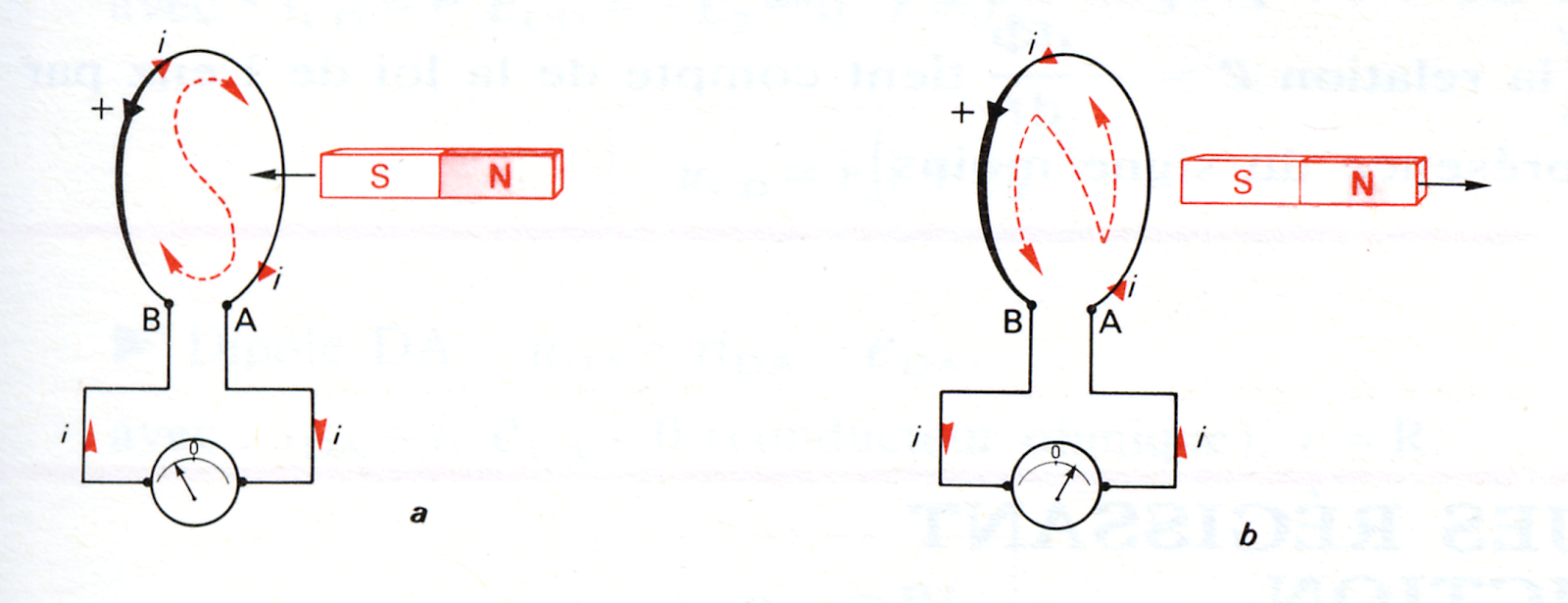
قانون لانز : إن جهة التيار المتحرض تكون بحيث تعاكس الأفعال التي ينتجها السبب الذي أحدثها .
القوة المحركة الكهربائية المتحرضة : بينت التجارب السابقة أن :
القوة المحركة الكهربائية المتحرضة e :
- تتناسب طردا مع التغير في التدفق المغناطيسي المحرض ΔΦ عبر الدارة .
- تتناسب عكسيا مع المدة Δt التي يحدث فيها هذا التغير .
تعطى القوة المحركة الكهربائية المتحرضة المتوسطة بالعلاقة :
خلاصة :
- قوة ←( عزم أي دوران ) + حقل مغناطيسي ← قوة محركة كهربائية (تيار)← مبدأ مولدة
- تيار كهربائي + حقل مغناطيسي ← قوة ( عزم أي دوران ) ←مبدأ محرك
10- الدارات المغناطيسية بالتيار المستمر:
10-1 تعريف و هدف من الدارات المغناطسية :
تحتاج آلات تيار الكهربائي إلى حقل مغناطيسي مرتفع ( عامة أكبر من 1 T) للحصول على :
- إستطاعة كتلية W/kg) ) أكبر ما يمكن في المحركات .
- قوة جذب شديدة في كهرومغناطيسي (مغناطيس كهربائي ) .
للحصول على ذلك الحقل B لابد من إضافة للوشائع المولدة للحقل دارة عبارة عن نواة من الفولاذ حديدية التمغنط بحيث تكون الأحسن مغلقة .
الدارة المغناطيسية عبارة عن مجموعة أوساط تحتوي أساسا على مواد حديدية التمغنط تشكل دارة مغلقة ويمكن أن يعبرها تدفق مغناطيسي .
أمثلة لدارات مغناطيسية :
المغانط الكهربائية : مغناطيس كهربائي هوعبارة عن مغناطيس كهربائي مؤقت لاينتج تأثيرات مغناطيسية ملحوظة إلا إذا كانت الوشيعة مجتازة بالتيار . يحتوي على الأقل على نواة ممغنطة من الحديد أو الفلاذ اللين وحولها وشيعة أوعدة وشائع ممغنطة .يمكنه جذب قطع حديدية التمغنط تسمى لابوس armature .
11- مبدأ مرحل كهرومغناطيسي :
المرحل هو عبارة عن مركب كهرومغناطيسي يسمح بفتح وغلق قاطعة كهربائية بإشارة تحكم . يحتوي على جزئين مستقلا كهربائيا ، لكن مقرونة كهروميكانيكيا :
- جزء التحكم يحتوي على وشيعة .
- قاطعة أو عدة قواطع متحكم فيها .
ع