العالم الاسلامي السنة الأولى ثانوي

سلسلة تمارين حول السقوط على مستوى مائل 

المادة	علوم فيزيائية
المستوى	السنة الثالثة ثانوي
الشعبة	علوم تجريبية , تقني رياضي , رياضيات
الوحدة	تطور جملة ميكانكية
نوع الملف	doc
صاحب الملف	.....
تحميل	سلسلة تمارين االسقوط على مستوى مائل

تمارين حول الحركة على المستوى المائل و المستوى الأفقي

التمرين 01 : BAC 2012 ( ر + ت ر )

1 – لغرض حساب زاوية الميل α لمستو يميل عن الأفق، قام فوج من التلاميذ بقذف جسم صلب (S) كتلته m = 1 kg في اللحظة t = 0 من النقطة O بسرعةV  نحو الأعلى وفق خط الميل الأعظم لمستو أملس ( الشكل – 4 ). باستعمال تجهيز مناسب، تمكن التلاميذ من دراسة حركة مركز عطالة (S) والحصول على أحد مخططات السرعة  v =f(t) أ – بتطبيق القانون الثاني لنيوتن، ادرس طبيعة حركة الجسم (S) بعد لحظة قذفه من O. ب – من بين المخططات الأربعة  ، ‚ ، ƒ ، „ ، ما هو المخطط الموافق لحركة الجسم (S)؟ علل. ج – احسب قيمة الزاوية α. د – احسب المسافة المقطوعة بين اللحظتين t = 0 و t = 2s. 2 – في الحقيقة يخضع الجسم أثناء انزلاقه على       المستوي المائل إلى قوة احتكاك شدتها ثابتة f. أ – أحص ومثّل القوى الخارجية المؤثرة على الجسم (S). ب – ادرس حركة مركز عطالة (S).        ثم استنتج العبارة الحرفية لتسارع حركته. ج – احسب قيمة التسارع من أجل f = 1,8N. تعطى: g = 9,8 m.s-2.

التمرين 02 : BAC 2011 ( ر + ت ر )

يجر جسم صلب (S2) كتلته m2 = 600g بواسطة خيط مهمل الكتلة وعديم الامتطاط يمر على محز بكرة مهملة الكتلة ، عربة (S1) كتلتها m1 = 800g تتحرك على مستو يميل عن الأفق بزاوية α = 30°. في وجود قوى احتكاك  شدتها ثابتة ولا تتعلق بسرعة العربة. في اللحظة t = 0s تنطلق العربة من النقطة A دون سرعة ابتدائية، فتقطع مسافة AB = x، كما هو موضح في (الشكل – 4). نأخذ كمبدأ للفواصل النقطة A. 1 – أعد رسم الشكل – 4، أحص ومثّل عليه القوى       الخارجية المؤثرة على كل من (S1) و (S2). 2 – بتطبيق القانون الثاني لنيوتن على (S1) و (S2).     أ – بيّن أن المعادلة التفاضلية للفاصلة x تعطى بالعلاقة التالية    ب – استنتج طبيعة حركة الجسم (S1).     ج – باستغلال الشروط الابتدائية أوجد حلا للمعادلة التفاضلية السابقة. 3 – من أجل قيم مختلفة لـ x كررنا التجربة السابقة عدة مرات فتحصلنا على منحنى بياني يلخص طبيعة حركة الجسم (S1).     أ – من بين البيانات  ، ‚ ، ƒ ما هو البيان الذي يتفق مع الدراسة النظرية السابقة؟ علل.    ب – احسب من البيان قيمة التسارع a.     ج – استنتج قيمة كل من قوة الاحتكاك f وتوتر الخيط T. علما أن g = 9,80 m.s-1.

التمرين 03 : BAC 2011 ( ر + ت ر )

عامل في أحد المخازن ، يدفع صندوقا كتلته m = 20kg، على مستوي أفقي إلى أن تبلغ سرعته حدا معينا، ثم يتركه لحاله، في لحظة نعتبرها مبدأ لقياس الأزمنة. اعتبارا من هذه اللحظة، يتحرك G مركز عطالة الصندوق على مسار  مستقيم حتى اللحظة t1، وفق المحور Ox. التطور الزمني لكل من الفاصلة x(t) والسرعة v(t) لمركز العطالة G، المبينين بالمنحنيين (الشكل-3).  نستخدم وحدات النظام الدولي SI. 1 - أ – تعرّف على المنحنى البياني الممثل للفاصلة x(t) والمنحنى البياني الممثل       للسرعة v(t).    ب – حدّد بيانيا قيمة اللحظة t1. ماذا يحدث للصندوق عندئذ؟ 2 – ارسم مخطط التسارع aG(t) للنقطة G. 3 – أ – مثل القوى الخارجية المؤثرة على الصندوق أثناء الحركة.    ب – بتطبيق القانون الثاني لنيوتن على مركز عطالة الصندوق، أوجد شدة قوة          الاحتكاك المؤثرة عليه. 4 – أ – اكتب المعادلة التفاضلية للسرعة على المحور Ox ، واستنتج المعادلة           الزمنية x(t) للحركة.    ب – استنتج بيانيا المسافة التي يقطعها مركز عطالة الصندوق بطريقتين مختلفتين.

التمرين 04 : BAC 2010 ( ر + ت ر )

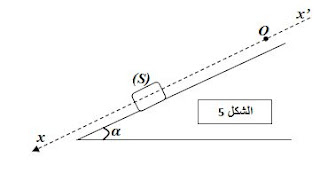
ينزلق جسم صلب (S) كتلته m = 100g على طول مستو مائل عن الأفق بزاوية α = 20° وفق المحور "xx ( الشكل – 5). قمنا بالتصوير المتعاقب بكاميرا رقمية (Webcam)، وعولج شريط الفيديو ببرمجية (Aviméca) بجهاز الإعلام الآلي وتحصلنا على النتائج التالية: 0,12 0,10 0,08 0,06 0,04 0,00 t(s) 0,32 0,28 0,24 0,20 0,16 v0 v(m.s-1) 1 – ارسم البيان v=f(t). 2 – بالاعتماد على البيان:        أ – بين طبيعة حركة (S).       ب – استنتج القيمة التجريبية للتسارع a.       ج – استنتج قيمة السرعة v0 في اللحظة t=0.        د – احسب المسافة المقطوعة بين اللحظتين:         ( t1 = 0,04s  و  t2 = 0,08s ). 3 – بفرض أن الاحتكاكات مهملة:     أ – بتطبيق القانون الثاني لنيوتن أوجد العبارة          الحرفية للتسارع a0 ثم احسب قيمته.     ب – قارن بين a0 و a. كيف تبرر الاختلاف؟ 4 – أوجد شدة القوة  المنمذجة للاحتكاكات على ول المستوي المائل. يعطى: g = 10 m.s-2  ؛  sin 20° = 0,34

التمرين 05 : BAC 2008 ( ر + ت ر )

ورد في مطوية أمن الطرق الجدوّل التالي: 110 100 90 80 50 v(km.h-1) سرعة السيارة 31 28 25 22 14 d1(m) مسافة الاستجابة 67 55 45 35 14 d2(m) المسافة الموافقة لمدة الكبح عندما يهم(يريد) سائق سيارة تسير بسرعة v بالتوقف، فإن السيارة تقطع مسافة (d1) خلال مدة (T1) قبل أن يضغط السائق على المكابح [ تعرف (T1) بزمن استجابة السائق]. وتقطع السيارة مسافة (d2) خلال مدة (T2) زمن مدة الكبح. تسمى (D) مسافة التوقف وتساوي مجموع المسافتين (d1 d2): D = d1+d2. أثناء عملية الكبح لا يؤثر المحرك على السيارة.  نقوم بدراسة حركة G ( مركز عطالة سيارة كتلتها M) على طريق مستقيمة أفقية في مرجع أرضي. نعتبره غاليليا. 1 – خلال مدة الاستجابة (T1)، نعتبر المجموع الشعاعي للقوى المؤثرة على السيارة معدوما.     أ – ما هي طبيعة حركة مركز عطالة السيارة؟    ب – استنادا إلى قياسات الجدل احسب قيم النسب d1/V . ماذا تستنتج؟     ج – احسب قيمة المدة (T1) ( مقدرة بالثانية )، من أجل كل قيمة لـ (d1) في الجدوّل. 2 – أ – ننمذج – خلال عملية الكبح – الأفعال المؤثرة على السيارة بقوى تطبق على مركز عطالتها. نعتبر القوى ( قوة الكبح وقوى الاحتكاكات ومقاومة الهواء ) المؤثرة على السيارة مكافئة لقوة واحدة  ثابتة في القيمة، وجهتها عكس جهة شعاع السرعة.    ب – لتكن v قيمة سرعة مركز عطالة السيارة في بداية الكبح. أوجد العلاقة الحرفية بين v2 و d2 بتطبيق مبدأ انحفاظ الطاقة.   ج – باستعمال الجدوّل السابق، ارسم المنحنى البياني v2=g(d2).   د – باستغلال البيان، استنتج قيمة تعطى كتلة السيارة: M = 9,0×102 kg

التمرين 06 : BAC 2008 ( ر + ت ر )

نهمل تأثير الهواء وكل الاحتكاكات. يترك جسم نقطي (S)، دون سرعة ابتدائية من النقطة A لينزلق وفق خط الميل الأعظم AB لمستو مائل يصنع مع الأفق زاوية α = 30°. المسافة ( AB = L ). يتصل AB مماسيا في النقطة B بمسلك دائري (BC) مركزه (O) ونصف قطره (r) بحيث تكون النقاط A،B،C،O ضمن نفس المستوي الأفقي.(الشكل-2). يعطى: كتلة الجسم m = 0,2 kg  ،  g = 10 m.s-2  ،  L = 5 m  ،  r = 2 m 1 – أوجد عبارة سرعة الجسم (S) عند مروره       بالنقطة B بدلالة L،g،α. ثم احسب قيمتها. 2 – حدد خصائص شعاع السرعة للجسم (S) في النقطة C. 3 – أ – أوجد بدلالة m،g،α عبارة شدة القوة التي تطبقها       الطريق على الجسم (S) خلال انزلاقه على المستوي       المائل. احسب قيمتها.      ب – لتكن I أخفض نقطة من المسار الدائري (BC).      يمر الجسم (S) بالنقطة I بالسرعة vI = 7,37 m.s-1.     احسب شدة القوة التي تطبقها الطريق على الجسم (S) عند النقطة I. 4 – عند وصول الجسم (S) إلى النقطة C يغادر المسار (BC) ليقفز في الهواء.     أ – أوجد في المعلم  المعادلة الديكارتية y = f(x) لمسار الجسم (S).          نأخذ مبدأ الأزمنة ( t=0 ) لحظة مغادرة الجسم النقطة C.    ب – يسقط الجسم (S) على المستوي الأفقي المار بالنقطتين B ، C في النقطة M. احسب المسافة CM.